
Формула Z Score (Оглавление)
- формула
- Примеры
- Калькулятор
Что такое формула Z баллов?
«Z-балл» является одним из наиболее широко используемых статистических инструментов, который используется для стандартизации балла, при условии, что популяционные средние и стандартное отклонение известны. Таким образом, оценка Z также известна как стандартная оценка. Оценка Z варьируется в диапазоне от -3 раз стандартного отклонения до +3 раз стандартного отклонения со средним значением нуля и стандартным отклонением единица. Формула для оценки Z для переменной может быть получена путем вычитания среднего значения совокупности из заданной переменной (которая является частью набора данных или совокупности), а затем деления результата на стандартное отклонение совокупности. Математически это представляется как
Z = (X – μ) / σ
где,
- X = переменная от населения
- μ = средняя численность населения
- σ = стандартное отклонение населения
Примеры формулы Z-баллов (с шаблоном Excel)
Давайте рассмотрим пример, чтобы лучше понять расчет Z Score.
Вы можете скачать этот шаблон Z Score Formula Excel здесь - Шаблон Z Z Formula ExcelФормула Z Score - Пример № 1
Давайте возьмем пример Мэнни, который недавно появился на SAT. Ему удалось набрать 1109 в этой попытке. Однако, согласно имеющейся информации, средний балл по SAT оставался около 1030 со стандартным отклонением 250. Вычислите Z балл по баллу SAT Мэнни и оцените, насколько хорошо он справился, по сравнению со средними тестируемыми.
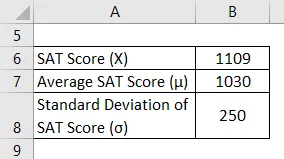
Решение:
Z Score рассчитывается по формуле, приведенной ниже
Z = (X - μ) / σ
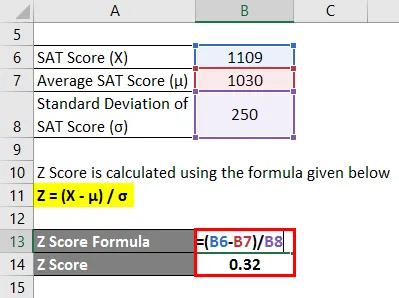
- Z Score = (1109 - 1030) / 250
- Z балл = 0, 32
Таким образом, балл SAT Мэнни на 0, 32 стандартного отклонения выше среднего балла тестируемых, что указывает на то, что 62, 55% тестируемых набрали меньше, чем Мэнни.
Формула Z Score - Пример № 2
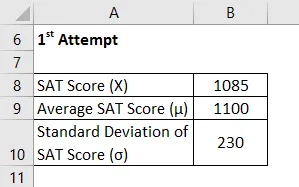
Теперь давайте возьмем пример Челси, который дважды написал SAT и хочет сравнить ее результаты в них. Ей удалось набрать 1085 и 1059 в ее 1- й и 2- й попытках соответственно. Согласно имеющейся информации, средний балл и стандартное отклонение во время 1- й попытки были 1100 и 230 соответственно, тогда как в последней это были 1050 и 240 соответственно. Пожалуйста, помогите Челси решить, на каком экзамене она выступила лучше.
Решение:
1- я попытка
Z Score рассчитывается по формуле, приведенной ниже
Z = (X - μ) / σ
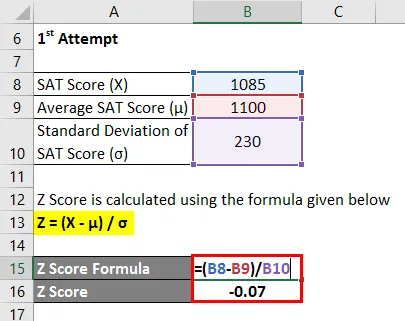
- Z Score = (1085 - 1100) / 230
- Z балл = -0, 07
Таким образом, оценка SAT «Челси» в 1- й попытке на 0, 07 стандартного отклонения ниже, чем средняя оценка тестируемых, что указывает на то, что 47, 40% тестируемых набрали меньше, чем «Челси» во время 1- й попытки.
2- я попытка
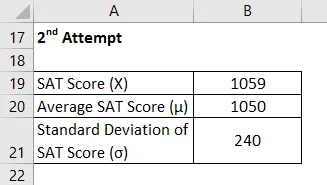
Z Score рассчитывается по формуле, приведенной ниже
Z = (X - μ) / σ
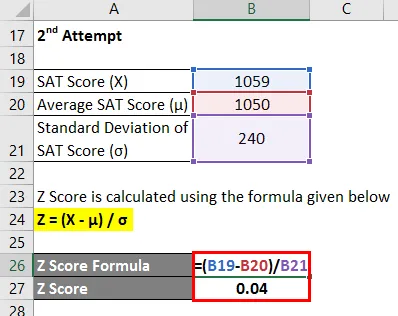
- Z Score = (1059 - 1050) / 240
- Z балл = 0, 04
Таким образом, оценка SAT «Челси» во 2- й попытке на 0, 04 стандартного отклонения выше, чем средняя оценка тестируемых, что указывает на то, что 51, 50% участников набрали меньше, чем «Челси» во 2- й попытке.
Таким образом, из сравнения результатов Z видно, что «Челси» выступил лучше во время 2- й попытки.
объяснение
Формула для оценки Z может быть получена с помощью следующих шагов:
Шаг 1: Во-первых, создайте совокупность с большим количеством переменных, и переменные будут обозначены X i .
Шаг 2: Далее рассчитывается количество переменных в популяции и обозначается как N.
Шаг 3: Затем среднее значение популяции рассчитывается путем суммирования всех переменных с последующим делением на общее количество переменных (шаг 2) в наборе данных. Средняя численность населения обозначается через µ.
μ = ∑ X i / N
Шаг 4: Затем вычтите среднее значение из каждой переменной набора данных, чтобы рассчитать их отклонение от среднего.
т.е. (X i - μ) является отклонением для i- й точки данных.
Шаг 5: Затем вычислите квадратичные отклонения для переменных, т.е. (X i - μ) 2 .
Шаг 6: Затем сложите все квадратичные отклонения и затем разделите общее количество на количество переменных в наборе данных, чтобы получить дисперсию.
σ 2 = ∑ (X i - μ) 2 / N
Шаг 7: Затем стандартное отклонение совокупности рассчитывается путем вычисления квадратного корня из дисперсии, рассчитанной на предыдущем этапе.
σ = √ ∑ (X i - μ) 2 / N
Шаг 8: Наконец, формула для оценки Z получается путем вычитания среднего значения популяции (шаг 3) из переменной и последующего деления результата на стандартное отклонение популяции (шаг 7), как показано ниже.
Z = (X - μ) / σ
Актуальность и использование формулы Z баллов
С точки зрения статистики, концепция Z-показателя очень важна, так как она полезна для определения вероятности того, произойдет ли событие в нормальном распределении. Фактически, Z-оценка также используется для сравнения двух необработанных оценок из двух разных нормальных распределений, и это делается путем преобразования необработанных оценок в Z-оценку или стандартизированную оценку. Кроме того, положительная оценка Z подразумевает оценку выше среднего, в то время как отрицательная оценка Z означает оценку ниже среднего.
Калькулятор формулы Z Score
Вы можете использовать следующий калькулятор формулы Z Score
| Икс | |
| μ | |
| σ | |
| Z | |
| Z = |
|
|
Рекомендуемые статьи
Это было руководство к формуле Z баллов. Здесь мы обсудим, как рассчитать Z Score вместе с практическими примерами. Мы также предоставляем калькулятор Z Score с загружаемым шаблоном Excel. Вы также можете посмотреть следующие статьи, чтобы узнать больше -
- Примеры формулы размера образца
- Как рассчитать взвешенное среднее?
- Калькулятор формулы корреляции
- Формула для расчета нормального распределения
- Примеры оценки Альтмана Z