
Составная формула годового темпа роста (Содержание)
- формула
- Примеры
- Калькулятор
Что такое формула составного годового роста?
Сложность - это эффект, когда инвестиции приносят проценты не только по основному компоненту, но и по процентам. Таким образом, сложный годовой темп роста - это эффективный годовой рост, полученный на инвестициях, с учетом сложившейся картины. Это в основном предполагает, что проценты, заработанные каждый год, реинвестируются, и они получают те же проценты, что и основная сумма. Это причина того, что совокупный годовой темп роста всегда выше, чем простая процентная ставка. Многие инвестиции, такие как паевые инвестиционные фонды, доходность фондового рынка не очень линейны и очень нестабильны.
Сложный годовой темп роста помогает сгладить эту прибыль и покажет, сколько инвестор заработал за период инвестиций, учитывая тот факт, что все доходы за этот период реинвестируются с одинаковой скоростью. Благодаря этому сглаживающему эффекту он помогает нам сравнивать наборы данных с различным уровнем волатильности. Это очень часто используется с целью финансового анализа.
Конечная сумма инвестиций = начальная сумма (1 + CAGR) количество лет
Формула для сложного годового темпа роста -
CAGR = (Ending Investment Amount / Start Amount) (1 / Number of Years) – 1
Эта формула применима, если инвестиции накапливаются ежегодно, это означает, что мы реинвестируем деньги на ежегодной основе. Но иногда случается так, что мы хотим вычислить скорость, с которой происходит сложение, на ежеквартальной, ежемесячной, ежедневной основе. Для этого мы используем следующую формулу:
Конечная сумма инвестиций = начальная сумма (1 + CAGR / частота составления) (количество лет * частота составления)
Итак, формула для совокупного годового темпа роста -
CAGR = Compounding Frequency * ((Ending Investment Amount / Start Amount) (1 / (Number of Years * Compounding Frequency)) – 1)
Частота смешивания:
- Полугодовое соединение: 2
- Ежеквартальное соединение: 4
- Ежемесячная частота: 12 и так далее
Примеры формулы CAGR (с шаблоном Excel)
Давайте рассмотрим пример, чтобы лучше понять расчет формулы CAGR.
Вы можете скачать этот шаблон Excel для составного годового роста здесь - Шаблон Excel для составного годового ростаCAGR Formula - Пример № 1
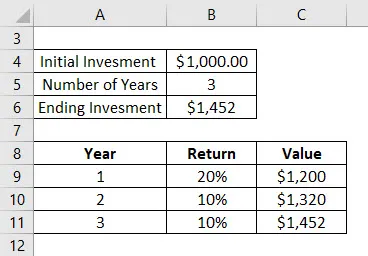
Допустим, вы вложили 1000 долларов во взаимные фонды 3 года назад. Ниже приводится доход, который вы получили за эти 3 года:
- 1- й год вы получаете увеличение стоимости на 20%. Таким образом, общая стоимость составляет 1200 долларов на конец 1- го года
- 2- й год вы получили 10% прироста стоимости. Таким образом, общая стоимость $ 1320 на конец 2- го года
- 3- й год вы получаете 10% прирост стоимости. Таким образом, общая стоимость $ 1452 на конец третьего года
CAGR рассчитывается по формуле, приведенной ниже
CAGR = (конечная сумма инвестиций / начальная сумма) (1 / количество лет) - 1
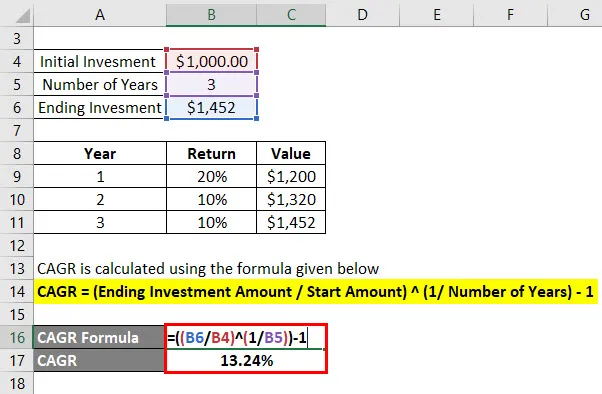
- CAGR = (1 452 долл. США / 1 000 долл. США) (1/3) - 1
- CAGR = 13, 24%
Здесь мы видим, что годовой доход за все 3 года различен и различен, но совокупный годовой темп роста дает нам единый показатель, который мы можем сравнить с различными инвестиционными возможностями.
CAGR Formula - Пример № 2
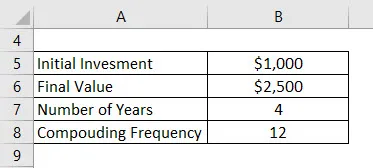
Допустим, вы вложили в банк 1000 долларов и хотите хранить деньги в банке в течение 4 лет. Теперь допустим, что общая сумма, которую вы получите через 4 года, составляет 2500 долларов. Банк предлагает ставку с ежемесячным начислением. Рассчитать CAGR.
CAGR рассчитывается по формуле, приведенной ниже
CAGR = частота смешивания * ((конечная сумма инвестиций / начальная сумма) (1 / (количество лет * частота смешивания)) - 1)
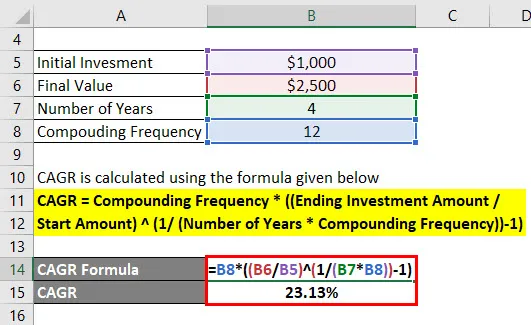
- CAGR = 12 * ((2500 долл. США / 1000 долл. США) (1 / (4 * 12)) - 1)
- CAGR = 23, 13%
Таким образом, совокупный годовой темп роста составляет 23, 13%.
Объяснение формулы сложного годового роста
Хотя совокупный годовой темп роста является годовым показателем для инвестиций, он является лишь теоретическим показателем и не является истинным доходом. Основное предположение здесь заключается в том, что все доходы реинвестируются с одинаковой ставкой в течение инвестиционного периода, но ставка не будет сохраняться в течение всех лет, и мы не можем инвестировать наши деньги по одной и той же ставке. Таким образом, это единственная репрезентативная ставка, которая говорит нам, что мы можем получить, если все деньги будут реинвестированы в конце каждого года по этой ставке. Таким образом, есть некоторые ключевые моменты, которые мы должны учитывать при использовании составного годового темпа роста.
Кроме того, мы будем очень осторожны с инвестициями, которые являются долгосрочными. Например, если инвестиционный период очень длинный, скажем, 20 лет, составная годовая процентная ставка может дать нам неверный признак, потому что может случиться так, что мы не получим никакой прибыли в течение первых 15 лет, и все доходы приходят в последний период, Получение прибыли в течение 15 лет неприемлемо для любого бизнеса.
Точно так же, если две инвестиционные возможности имеют один и тот же CAGR, может случиться так, что одна из них будет более привлекательной, чем другая, по той причине, что рост одной из них происходит в начальный период, в то время как для другой она концентрируется в конце период.
Актуальность и использование формулы составного годового темпа роста
Составной годовой темп роста действительно полезен для расчета среднего темпа роста инвестиций и может помочь в сравнении различных инвестиций. Как мы видели в приведенном выше примере, ежегодный рост инвестиций является неравномерным и неустойчивым. Но с учетом сложного годового темпа роста доходность сглаживается. Еще один фактор, который делает сложный годовой темп роста критическим методом при определении роста инвестиций, заключается в том, что он учитывает эффект сложного эффекта, а не годовой доход. Сложная годовая ставка не дает нам реальной картины доходности, поскольку она только рассчитывает доход по основной сумме и игнорирует процентную ставку по процентам, но это не относится к совокупной годовой ставке роста.
Составной годовой калькулятор формулы роста
Вы можете использовать следующий Составной годовой калькулятор темпов роста
| Конечная сумма инвестиций | |
| Начальная сумма | |
| Количество лет | |
| CAGR | |
| CAGR = | ((Конечная сумма инвестиций / Начальная сумма) 1 / Количество лет -1) |
| знак равно | ((0/0) 1/0 -1) = 0 |
Рекомендуемые статьи
Это было руководство к составной формуле годового роста. Здесь мы обсудим, как рассчитать CAGR вместе с практическими примерами. Мы также предоставляем калькулятор сложного годового роста с загружаемым шаблоном Excel. Вы также можете посмотреть следующие статьи, чтобы узнать больше -
- Руководство по формуле нормы прибыли
- Примеры формулы экспоненциального роста
- Калькулятор для формулы центральной предельной теоремы
- Как рассчитать рыночную капитализацию?