Введение в сортировку кучи в C
Сортировка - это метод упорядочения элементов на основе различных свойств. (Свойства, такие как расположение данных в порядке возрастания, убывания или в алфавитном порядке). Одним из основных примеров сортировки, о котором мы можем здесь подумать, является заказ товаров во время онлайн-покупок. Мы можем относиться к ценам, популярности, последней и так далее. Таким образом, существует много методов для позиционирования элементов посредством сортировки. В этой теме мы собираемся узнать о сортировке кучи в C.
Здесь мы собираемся изучить один из самых распространенных методов сортировки, Heap Sort, через язык программирования C.
Логика для кучи
Как на самом деле мы можем выполнить сортировку кучи? Давайте проверим ниже.
Во-первых, куча является одной из древовидных структур данных. Используемое здесь дерево всегда является Полным двоичным деревом. И есть два вида кучи
- Min - Heap: обычно размещается в порядке возрастания, то есть если элемент родительского узла имеет значение меньше значения элементов дочернего узла.
- Макс. - куча: как правило, в порядке убывания, то есть если родительский узел имеет значение больше, чем у дочерних узлов.
Шаги для сортировки кучи
- После получения несортированных данных списка элементы организуются в структуру данных кучи либо на основе создания минимальной кучи, либо максимальной кучи.
- Первый элемент из списка выше добавлен в наш массив
- Снова формируется техника структуры данных заголовка, аналогичная первой, и снова либо самый высокий элемент, либо наименьший элемент выбирается и добавляется в наш массив.
- Повторные шаги помогают нам получить массив с отсортированным списком.
Программа для сортировки кучи в C
#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)
Сначала мы просим пользователя ввести количество элементов, которые будут взяты для сортировки, а затем пользователю разрешено вводить различные элементы, которые должны быть отсортированы.
Шаги следовали
- Следующее, на чем мы сконцентрируемся, это создание массива кучи, в данном случае, массива max-heap.
- Основным условием получения массива max - heap является проверка того, что значение родительского узла не меньше значения его дочернего узла. Мы будем менять местами, пока не достигнем этого условия.
- Основным преимуществом этого полного двоичного дерева является то, что левый и правый дочерние узлы родительского узла могут быть доступны со значениями 2 (i) + 1 и 2 * (i) + 2 значения соответственно. Где я родительский узел.
- Таким образом, таким образом, мы помещаем наш корневой узел, который содержит максимальное значение, в крайнее правое место конечного узла. И затем снова, следуя той же процедуре, так что следующий максимальный номер теперь становится корневым узлом.
- Мы будем следовать той же процедуре, пока в массиве кучи не останется только один узел.
- И затем мы организуем наш массив кучи для формирования идеального отсортированного массива в порядке возрастания.
- Наконец, мы печатаем отсортированный массив в выводе.
Выход:
Выход прилагается ниже.
Позвольте мне показать вам наглядное представление о событиях:
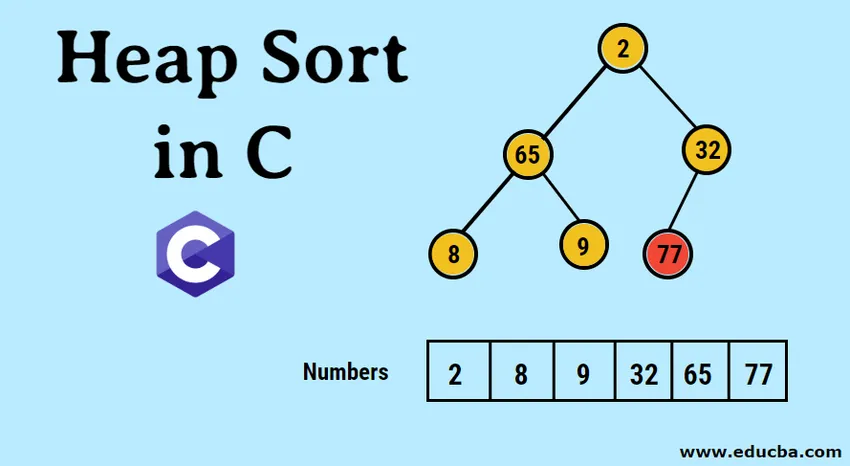
- Введенные данные сначала представляются в виде одномерного массива следующим образом.

- Графическое представление сформированного двоичного дерева выглядит следующим образом:
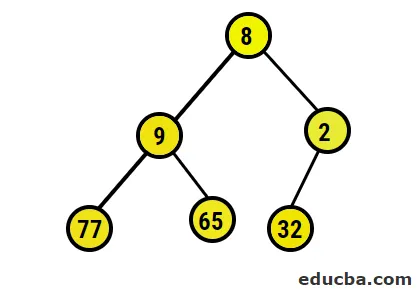
- Теперь мы собираемся преобразовать в максимальную кучу, убедившись, что все родительские узлы всегда больше, чем дочерние узлы. Как упомянуто в выходных данных в массиве, отсортированном по куче, графическое представление будет:
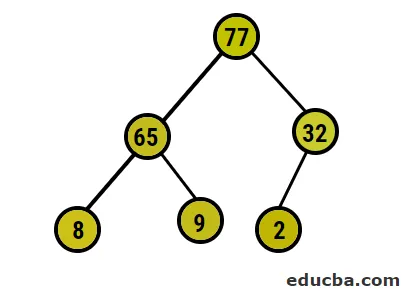
- После этого мы собираемся поменять местами корневой узел с крайним листовым узлом, а затем удалить его из дерева. Листовой узел будет корнем сейчас и снова тот же процесс e, чтобы снова получить самый высокий элемент в корне
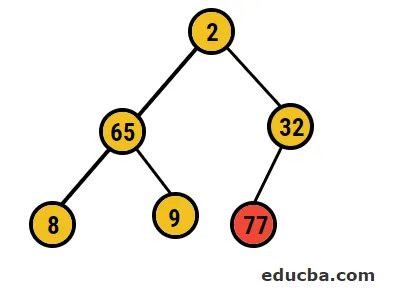
- Итак, в этом случае 77 цифр удаляются из этого дерева и помещаются в наш отсортированный массив, и процесс повторяется.
Выше мы видели это для формирования массива max heap. Тот же процесс имеет дело с формированием массива min-heap. Как обсуждалось выше, единственное различие заключается в отношении между элементами родительского и дочернего узла.
В качестве упражнения вы можете попробовать сформировать сортировку кучи в порядке убывания?
Вывод
Хотя существует много методов сортировки, сортировка кучи считается одной из лучших техник сортировки из-за сложности времени и пространства. Временная сложность для всех лучших, средних и наихудших случаев равна O (nlogn), где сложность наихудшего случая лучше, чем сложность Quicksort для наихудшего случая, а сложность пространства равна O (1).
Рекомендуемые статьи
Это руководство по сортировке кучи в C. Здесь мы обсудим логику и шаги по сортировке кучи с примером кода и вывода вместе с графическими представлениями. Вы также можете взглянуть на следующие статьи, чтобы узнать больше -
- Сортировка кучи в Java
- Выбор сортировки в Java
- Палиндром в программе C
- Шаблоны в C Программирование
- Сортировка кучи в C ++ (алгоритм)
- Сортировка кучи в Python
- C умножение матриц программирования