
Коэффициент вариационной формулы (Содержание)
- формула
- Примеры
Что такое коэффициент вариации?
В статистике коэффициент вариации также называется CV, это инструмент, который помогает нам определить, как точки данных в наборе данных распределены вокруг среднего значения. По сути, сначала отображаются все точки данных, а затем коэффициент вариации используется для измерения дисперсии этих точек друг от друга и среднего значения. Таким образом, это помогает нам понять данные, а также увидеть шаблон, который они формируют. Он рассчитывается как отношение стандартного отклонения набора данных к среднему значению. Чем выше коэффициент вариации, тем выше уровень разброса данных вокруг среднего. Аналогичным образом, чем ниже значение коэффициента вариации, тем меньше дисперсия и более точными будут результаты. Даже если среднее значение двух рядов данных значительно отличается, коэффициент вариации очень полезен для сравнения степени вариации от одного ряда данных к другому.
Формула для коэффициента вариации дается:
Coefficient of Variation = Standard Deviation / Mean
Шаги для расчета коэффициента вариации:
Шаг 1: Рассчитать среднее значение набора данных. Среднее значение - это среднее значение всех значений, которое можно рассчитать, взяв сумму всех значений, а затем разделив ее на число точек данных.
Шаг 2: Затем вычислите стандартное отклонение набора данных. Это немного трудоемкий процесс. Отклонение от нормы можно рассчитать как: √ (Σ (X i - X m ) 2 / (n - 1)) . X i является i -й точкой данных, а X m является средним значением набора данных. Кроме того, мы также можем найти стандартное отклонение в Excel, используя функцию STDEV.S ().
Шаг 3: Разделите стандартное отклонение на среднее, чтобы получить коэффициент вариации.
Примеры коэффициента формулы изменения (с шаблоном Excel)
Давайте рассмотрим пример, чтобы лучше понять расчет коэффициента вариации.
Вы можете скачать этот шаблон Excel формулы коэффициента вариации здесь - Коэффициент Excel шаблона формулы вариацииКоэффициент вариационной формулы - Пример № 1
Допустим, у нас есть два набора данных A & B, и каждый содержит 20 случайных точек данных. Рассчитать коэффициент вариации для набора данных X & Y.
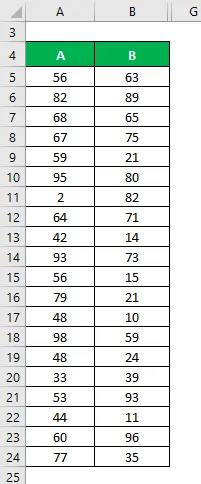
Решение:
Среднее значение рассчитывается как:
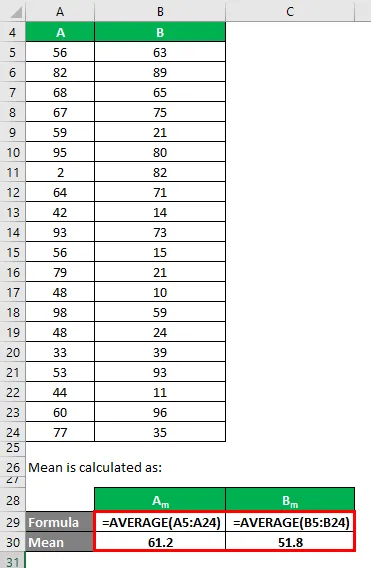
- Среднее значение набора данных A = 61, 2
- Среднее из набора данных B = 51, 8
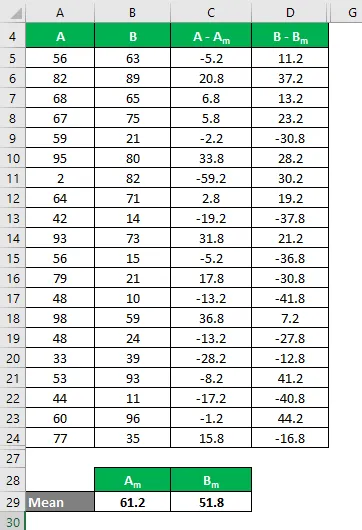
Теперь нам нужно вычислить разницу между точками данных и средним значением.
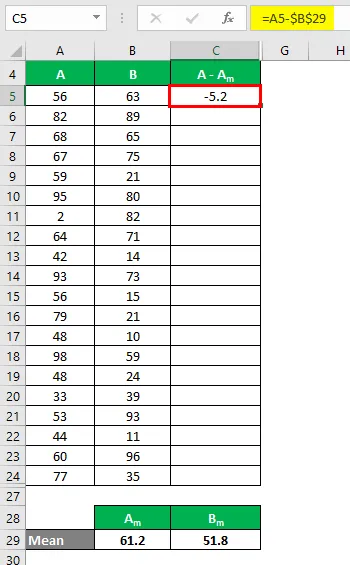
Аналогичным образом рассчитайте для всех значений набора данных A.
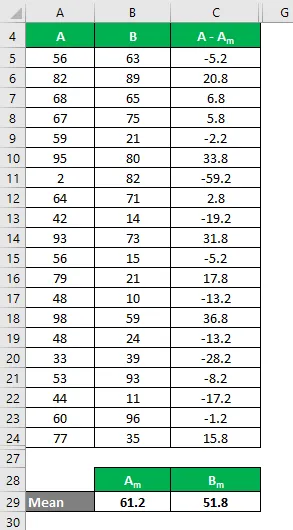
Аналогичным образом рассчитайте для всех значений набора данных B.
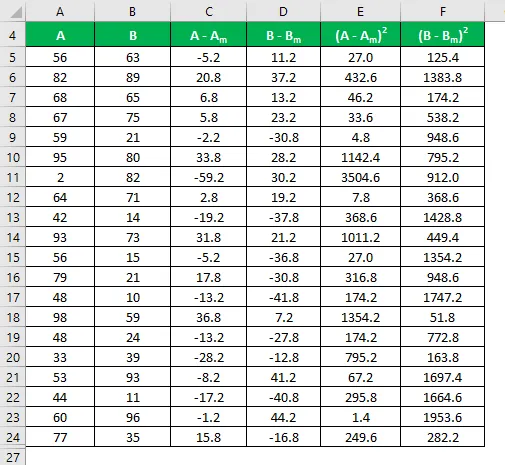
Рассчитайте квадрат разности для обоих наборов данных A и B.
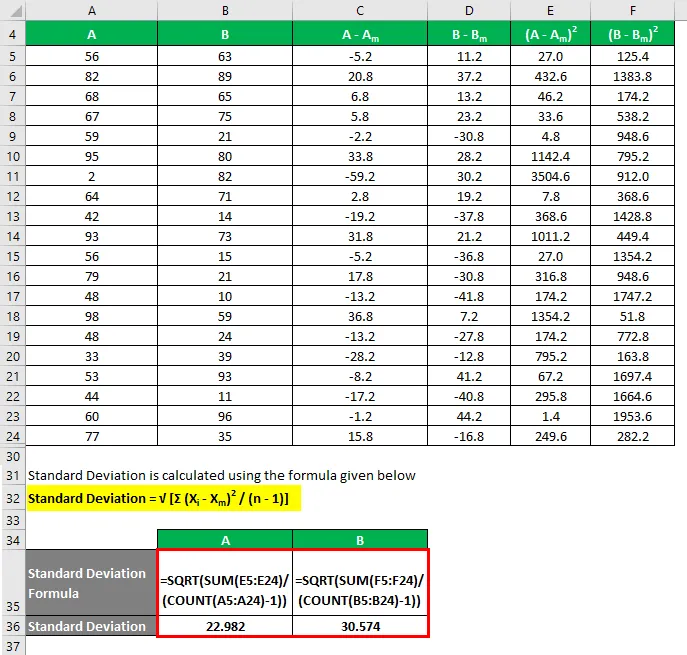
Стандартное отклонение рассчитывается по формуле, приведенной ниже
Стандартное отклонение = √ (Σ (X i - X m ) 2 / (n - 1))
Коэффициент вариации рассчитывается по формуле, приведенной ниже
Коэффициент вариации = стандартное отклонение / среднее
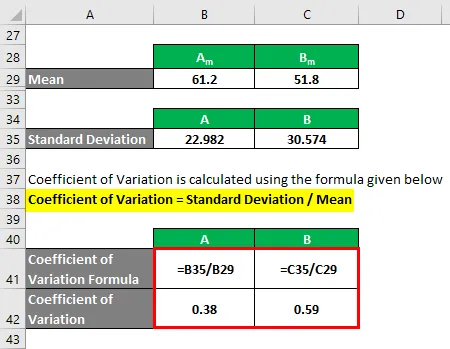
- Коэффициент вариации A = 22, 982 / 61, 2 = 0, 38
- Коэффициент вариации B = 30, 574 / 51, 8 = 0, 59
Таким образом, если вы видите здесь, B имеет более высокий коэффициент вариации, чем A, что означает, что точки данных B более рассеяны, чем A.
Коэффициент вариационной формулы - Пример № 2
Допустим, вы очень склонный к риску инвестор и хотите инвестировать деньги в фондовый рынок. Поскольку у вас низкий аппетит к риску, вы хотите инвестировать в безопасные акции с более низким стандартным отклонением и коэффициентом вариации. Вы выбрали 3 акции на основании их фундаментальной и технической информации и хотите выбрать 2 акции. Вы также собрали информацию об их исторических доходах за последние 15 лет.
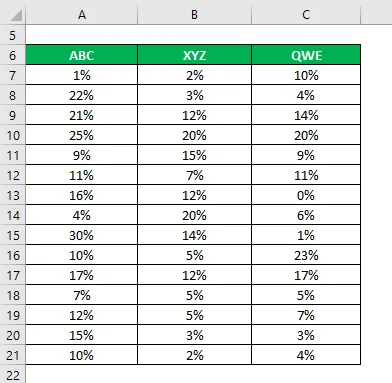
Решение:
Среднее значение рассчитывается как:
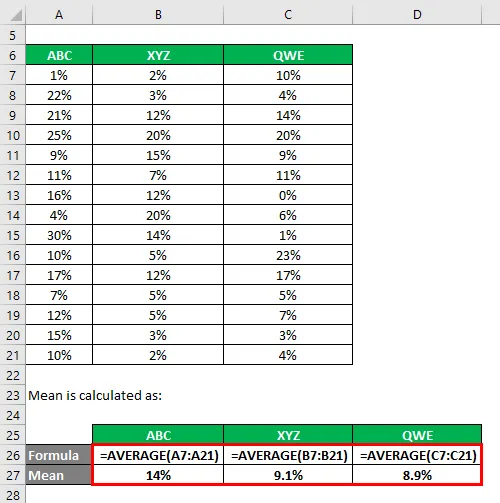
Стандартное отклонение рассчитывается по формуле Excel
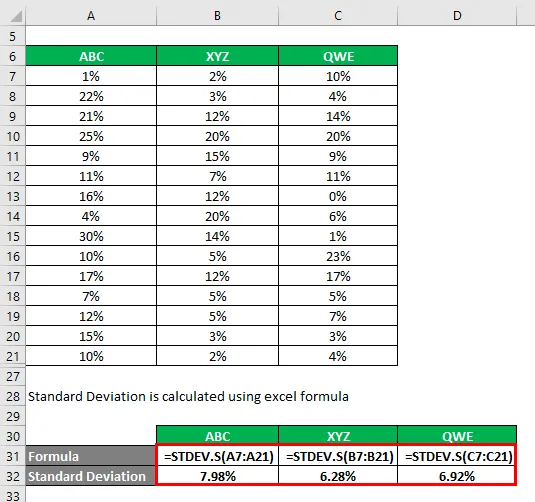
Коэффициент вариации рассчитывается по формуле, приведенной ниже
Коэффициент вариации = стандартное отклонение / среднее
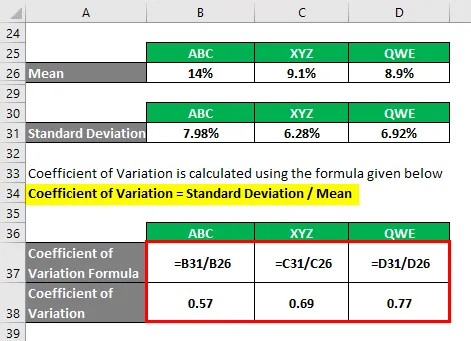
- Коэффициент вариации ABC = 7, 98% / 14% = 0, 57
- Коэффициент вариации XYZ = 6, 28% / 9, 1% = 0, 69
- Коэффициент вариации QWE = 6, 92% / 8, 9% = 0, 77
Основываясь на информации, вы выберете акции ABC и XYZ для инвестирования, поскольку они имеют самый низкий коэффициент вариации.
объяснение
Поскольку коэффициент вариации является мерой риска, он помогает измерять волатильность цен акций и других финансовых инструментов. Это также помогает инвесторам и аналитикам сравнивать риски, связанные с различными потенциальными инвестициями.
Коэффициент вариации аналогичен стандартному отклонению, но стандартное отклонение двух переменных не может быть сравнено по полезности. Но использование стандартного отклонения и среднего значения делает относительное сравнение более значимым. Существует также ограничение коэффициента вариации. Предположим, что среднее значение набора данных равно нулю. В этом случае этот инструмент станет неэффективным. Мало того, что если у нас есть набор данных, который имеет много положительных и отрицательных значений, коэффициент вариации становится очень проблематичным. Так что это более полезно только для наборов данных, имеющих одинаковый знак плюс-минус.
Актуальность и использование коэффициента вариационной формулы
Коэффициент вариации имеет значение во многих других областях, помимо статистики. Например, в области финансов коэффициент вариации является мерой риска. Это похоже на стандартное отклонение, поскольку оно также используется в качестве меры риска, но разница в том, что коэффициент вариации является лучшим индикатором относительного риска. Например, предположим, что ожидаемая доходность A составляет 15%, а ожидаемая доходность B - 10%, а стандартное отклонение A составляет 10%, а стандартное отклонение B - 5%. Чтобы выбрать лучшее вложение, можно использовать коэффициент вариации. Таким образом, коэффициент вариации A составляет 10/15 = 0, 666, а коэффициент вариации B составляет 5/10 = 0, 5. Таким образом, B - лучшая инвестиция, чем A.
Рекомендуемые статьи
Это было руководство к коэффициенту формулы изменения. Здесь мы обсудим, как рассчитать коэффициент вариации, используя формулу вместе с практическими примерами и загружаемым шаблоном Excel. Вы также можете посмотреть следующие статьи, чтобы узнать больше -
- Что такое скорректированная формула R в квадрате?
- Примеры коэффициента определения формулы
- Как рассчитать коэффициент корреляции по формуле?
- Ковариационная формула с шаблоном Excel