
Введение в математические функции в C
В этой статье перечислены различные математические функции, используемые в языках программирования C с иллюстрацией рабочего кода. Компьютеры выполняют огромные математические вычисления и анализ огромных чисел, для этого мы использовали математические функции в Си. Прежде чем начать, нам нужно знать, что языки Си используют заголовок / библиотеку с именем Math.h для различных математических функций. Это помогает в расчете тригонометрических операций, логарифмов, абсолютных значений, квадратных корней. Итак, давайте рассмотрим различные типы функций, используемых в этой библиотеке. Все эти функции принимают тип данных double и возвращают один и тот же.
Различные математические функции в C
Давайте рассмотрим различные функции, определенные в math.h, и библиотека Math подразделяется на три основных типа: тригонометрические функции, математические функции, функции Log / expo. Для реализации перечисленных ниже функций, обязательно включить или в код.
1. этаж (двойной)
Эта функция возвращает наибольшее целочисленное значение, не превышающее значение «a». Он округляет значение и в результате возвращает двойное число. Он ведет себя по-разному для отрицательных чисел, поскольку они округляются до следующего отрицательного числа.
Пример: этаж (7, 2) составляет 7, 0
пол (-7, 2) это -8, 0
Пример:
Эта программа иллюстрирует, как вычислить минимальное значение для заявленного значения и округлить до следующего значения 10.
#include
#include
int main()
(
double f= -9.33;
int final;
final = floor(f);
printf("Floor value of %.2f = %d", f, final);
return 0;
)
Выход:

2. ceil ()
Синтаксис:
double ceil (double b)
Эта функция возвращает наименьшее целочисленное значение, большее или равное b, и округляет значение в большую сторону. Для отрицательного значения он перемещается влево. Пример 3.4 возвращает -3 имеет вывод.
Пример:
Эта программа объясняет, принимая входные данные в аргументе float и возвращает значение ceil.
#include
#include
int main()
(
float n, ceilVal;
printf(" Enter any Numeric element : ");
scanf("%f", &n);
ceilVal = ceil(n);
printf("\n The Value of %.2f = %.4f ", n, ceilVal);
return 0;
)
Выход:

3. Sqrt ()
Эта функция возвращает квадратный корень указанного числа.
Синтаксис:
sqrt( arg)
Пример:
Приведенный ниже код объясняет наиболее известную математическую функцию sqrt (), принимая значения 'n' для вычисления квадратного корня для различных значений 'n'.
#include
#include
int main()
(
double n, output;
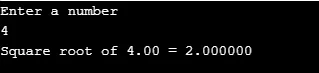
printf("Enter a number\n");
scanf("%lf", &n);
output = sqrt(n);
printf("Square root of %.2lf = %f", n, output);
return 0;
Выход:
4. круглый ()
Эта функция округляет ближайшее значение заданного входа. Выдает ошибку, если значение слишком велико. Другие функции, такие как lround (), llround (), также округляют ближайшее целое число.
Синтаксис:
int round(arg)
Пример:
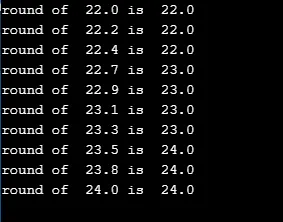
Приведенный ниже код очень прост и округляется до ближайшего значения 'r' в цикле for.
#include
#include
int main ()
(
for(double r=110;r<=120;r+=1.1)
printf("round of %.1lf is %.1lf\n", r/5.0, round(r/5.0));
return 0;)
Выход:
5.pow ()
Эта функция возвращается к власти для данного числа (a b ). Возвращает возведенный в степень b, который имеет два параметра base и exponent.
Пример:
В приведенном ниже исходном коде мы разрешаем пользователю вводить входное значение для вычисления мощности данных двух аргументов.
#include
#include
int main()
(
int r, ba, expr;
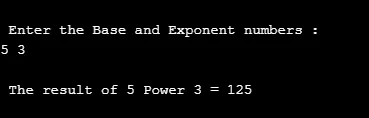
printf("\n Enter the Base and Exponent numbers : \n");
scanf("%d %d", &ba, &expr);
r = pow(ba, expr);
printf("\n The result of %d Power %d = %d ", ba, expr, r);
return 0;
)
выход:
6. trun ()
Эта функция помогает усечь данное значение. Возвращает целочисленные значения. Для усечения плавающих и двойных значений truncf (), truncl () используются.
Синтаксис:
double trunc(a);
Пример:
Ниже исходный код принимает два входных значения a, b для усечения двойных значений.
#include
#include
void main() (
double m, n, a, b;
a = 56.16;
b = 85.74;
m = trunc(a);
n = trunc(b);
printf("The value of a: %lf\n", m);
printf("The value of a: %lf\n", n);
)
Выход:

7. fmod ()
Эта функция возвращает остаток для заданных двух входных значений, когда m делится на n.
Синтаксис:
double fmod(double I, double j)
Пример:
В приведенном ниже примере от пользователя требуется два значения для вычисления остатка с помощью функции fmod ().
#include
#include
int main()(
double fiN;
double secN;
double n;
printf("Enter the first number : ");
scanf("%lf", &fiN);
printf("Enter the second number : ");
scanf("%lf", &secN);
printf("fmod(firstNumber, secondNumber) is %lf \n", fmod(fiN, secN));
)
Выход:

Тригонометрические функции
Ниже приведены различные функции тригонометрии:
1. грех ()
Эта встроенная функция дает синусоидальное значение заданного числа, вычисляет значения с плавающей точкой. asin () вычисляет дугу, для гиперболического это sinh ().
Синтаксис:
return type sin(y);
y возвращает значение в радианах, а тип возвращаемого значения удваивается.
Пример:
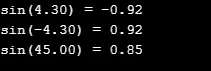
В следующем исходном коде я взял два разных входных значения для вычисления значения sin и возвращает значение double.
#include
#include
int main()
(
double a;
double z;
a = 4.3;
z = sin(a);
printf("sin(%.2lf) = %.2lf\n", a, z);
a = -4.3;
z = sin(a);
printf("sin(%.2lf) = %.2lf\n", a, z);
a = 45;
z = sin(a);
printf("sin(%.2lf) = %.2lf\n", a, z);
return 0;
)
Выход:
2. sinh ()
Эта математическая функция вычисляет тригонометрическое значение тангенса для заданного числа.
Синтаксис:
double sinh(x);
пример
В приведенном ниже исходном коде гиперболический синус вычисляется путем объявления входного значения.
#include
#include
#define PI 3.141592654
int main()
(
double gt = 3.60, z;
z = sinh(gt);
printf("Sine hyperbolic of %.2lf is = %.2lf", gt, z);
return 0;
)
Выход

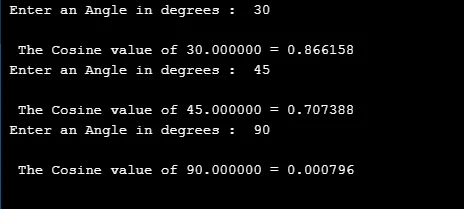
3. cos ()
Эта математическая функция определяет значение тригонометрического косинуса для данного элемента.
Синтаксис: return type cos(argument);
#include
#include
#define PI 3.14
int main()
(
double cVal, rVal, dVal;
for(int i=0;i<=2;i++)
(
printf(" Enter an Angle in degrees : ");
scanf("%lf", &dVal);
rVal = dVal * (PI/180);
cVal = cos(rVal);
printf("\n The Cosine value of %f = %f ", dVal, cVal);
printf("\n");
)
return 0;
)
Выход:
4. кош ()
Возвращает гиперболический косинус для заданного значения.
Синтаксис:
double cosh(y);
пример
В приведенном ниже примере показано, что для вычисления гиперболического значения требуются два разных входных значения.
#include
#include
int main ()
(
double k, r;
k = 0.6;
r = cosh(k);
printf("Hyperbolic cosine of %lf is = %lf\n", k, r);
k = -0.8;
r = cosh(k);
printf("Hyperbolic cosine of %lf is = %lf\n", k, r);
return 0;)
Выход

5. загар ()
Эта функция математической библиотеки вычисляет значения тангенса угла для математического выражения и измеряется в радианах.
Это может быть объявлено как
double tan(arguments);
пример
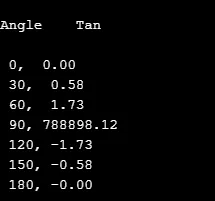
В следующем исходном коде значение tan рассчитывается для следующих углов, которые увеличиваются с помощью цикла for.
# include
# include
# include
void main()
(
float z ;
int k ;
char ch ;
printf("\nAngle \t Tan \n") ;
for (k = 0; k <= 180; k = k + 30)
(
z = k * 3.14159 / 180 ;
printf("\n %d, %5.2f", k, tan(z));
)
getch() ;
)
Выход:
6. tanh ()
Функция tanh () возвращает гиперболический тангенс заданного значения. Требуется один параметр. В дополнение к поиску тангенса для long double и float для вычисления используются tanhl () и tanhf ().
Синтаксис:
double tanh( val);
Пример:
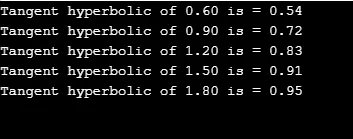
Касательная гиперболическая вычисляется для значений 'j' с использованием циклов for. Посмотрим, как это работает.
#include
#include
#define PI 3.141592654
int main()
(
double val, r;
for(double j=0.60; j<=2.0;j+=.30)
(
r = tanh(j);
printf("Tangent hyperbolic of %.2lf is = %.2lf", j, r);
printf("\n");
)
return 0;
)
Выход:
Логарифмические функции
Ниже приведены различные функции логарифмической арифметики:
1. exp ()
Эта функция выполняет вычисления по экспоненте для заданного значения (e x ). Есть также другие подтипы, такие как frexp (), Idexp (), возвращающие мантиссу и умноженные на степень x.
Синтаксис:
return type exp(value);
Пример:
Программа берет числовое значение от пользователя, чтобы вычислить показатель степени для данного значения и возвращает double.
#include
#include
int main()
(
double numb, eVal;
printf(" Enter any Numeric Value : ");
scanf("%lf", &numb);
eVal = exp(numb);
printf("\n Exponential Value of e power %lf = %lf ", numb, eVal);
printf("\n");
return 0;
)
Выход

2. войти ()
Эта функция возвращает логарифмическое значение заданного числа. (на базу е. войти е )
Синтаксис:
double log(arg);
Пример:
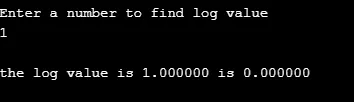
В следующем примере значение журнала для данного числа рассчитывается с использованием функции. Определяемая пользователем функция lgm () выполняет вычисления, и функция вызывается в основной функции.
#include
#include
float lgm ( float iv );
int main ()
(
float q, r ;
printf ( "\nEnter a number to find log value \n");
scanf ( "%f", &q ) ;
r = lgm ( q ) ;
printf ( "\nthe log value is %f is %f", q, r );
)
float lgm ( float iv ) // function definition
(
float exe ;
exe = log(iv);
return ( exe ) ;
)
выход:
Вывод
В заключение, мы видели различные математические функции, используемые в программировании на С, и это прямые библиотечные функции, которые нужно использовать. Программы на С используют эти функции для различных математических операций. Для решения некоторых сложных версий вычислений эта встроенная функция использует математически ориентированный язык программирования для возврата простых значений.
Рекомендуемые статьи
Это руководство по математическим функциям в C. Здесь мы обсуждаем различные математические функции в C с примерами. Вы также можете просмотреть наши другие предлагаемые статьи -
- PHP математические функции
- Математические функции JavaScript
- Функции передачи в Matlab
- Строковые функции JavaScript
- Введение в математические функции в Python
- Обзор математических функций в C #
- C умножение матриц программирования
- Квадратный корень в PHP
- Примеры квадратного корня в JavaScript