
Введение в алгоритм DFS
DFS известен как алгоритм поиска в глубину в первую очередь, который предоставляет шаги для прохождения каждого узла графа без повторения какого-либо узла. Этот алгоритм аналогичен первому обходу глубины для дерева, но отличается поддержанием логического значения для проверки, был ли узел уже посещен или нет. Это важно для обхода графа, поскольку в графе также существуют циклы. В этом алгоритме поддерживается стек для хранения приостановленных узлов во время обхода. Он назван так, потому что мы сначала перемещаемся на глубину каждого соседнего узла, а затем продолжаем проходить через другой соседний узел.
Объясните алгоритм DFS
Этот алгоритм противоречит алгоритму BFS, где посещаются все смежные узлы, за которыми следуют соседи к соседним узлам. Он начинает исследовать график с одного узла и исследует его глубину перед возвратом. В этом алгоритме учитываются две вещи:
- Посещение вершины: выбор вершины или узла графа для прохождения.
- Исследование вершины: Обход всех узлов, смежных с этой вершиной.
Псевдокод для поиска в глубину :
proc DFS_implement(G, v):
let St be a stack
St.push(v)
while St has elements
v = St.pop()
if v is not labeled as visited:
label v as visited
for all edge v to w in G.adjacentEdges(v) do
St.push(w)
Линейный обход также существует для DFS, который может быть реализован тремя способами:
- Предварительный заказ
- Чтобы
- PostOrder
Обратный порядок - очень полезный способ прохождения и используется в топологической сортировке, а также в различных анализах. Также поддерживается стек для хранения узлов, исследование которых еще не завершено.
Траверс графа в DFS
В DFS выполняются следующие шаги, чтобы пройти график. Например, для данного графа начнем обход с 1:
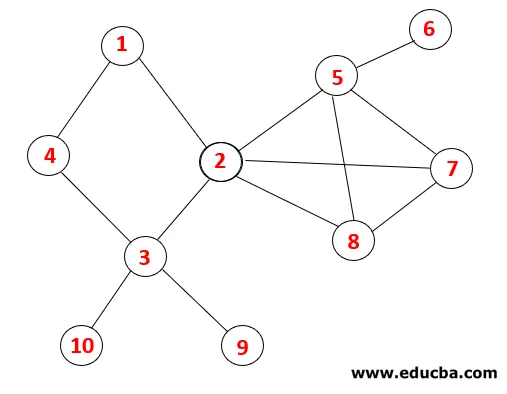
| стек | Последовательность обхода | Остовное дерево |
| 1 |  |
|
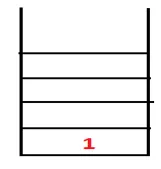 | 1, 4 |  |
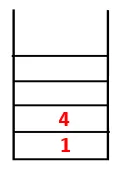 | 1, 4, 3 |  |
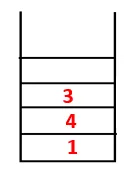 | 1, 4, 3, 10 | 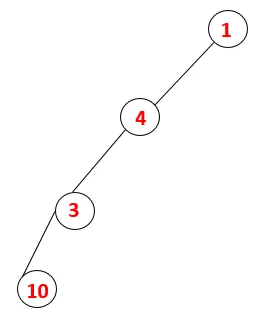 |
 | 1, 4, 3, 10, 9 | 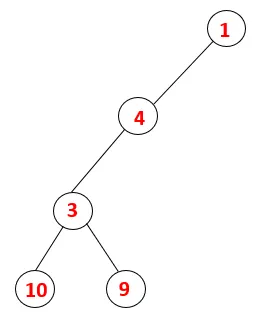 |
 | 1, 4, 3, 10, 9, 2 | 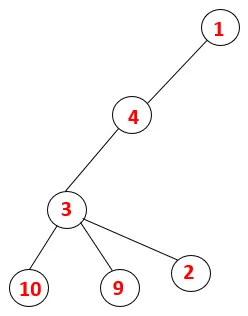 |
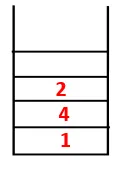 | 1, 4, 3, 10, 9, 2, 8 |  |
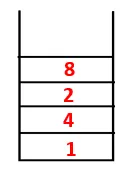 | 1, 4, 3, 10, 9, 2, 8, 7 | 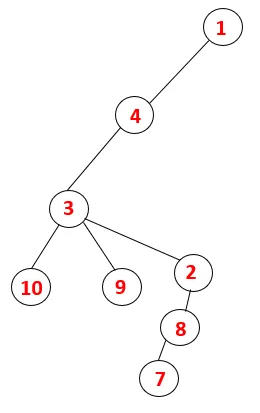 |
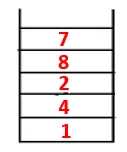 | 1, 4, 3, 10, 9, 2, 8, 7, 5 |  |
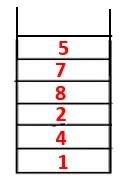 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 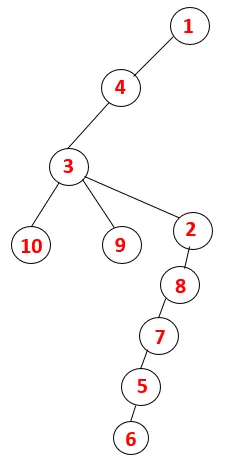 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 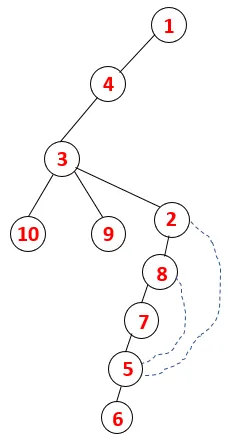 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
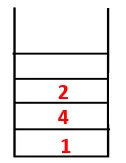 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 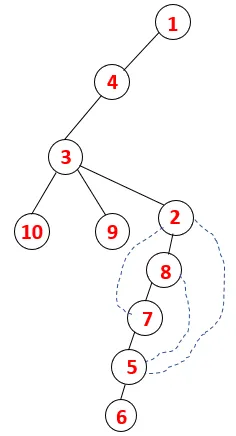 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 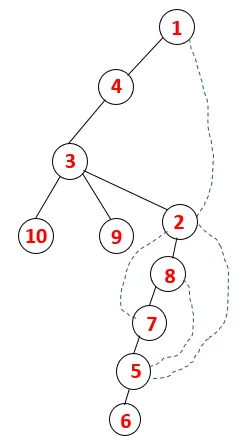 |
Пояснение к алгоритму DFS
Ниже приведены шаги к алгоритму DFS с преимуществами и недостатками:
Шаг 1: Узел 1 посещается и добавляется в последовательность, а также в связующее дерево.
Шаг 2: Исследуются смежные узлы 1, то есть 4, поэтому 1 помещается в стек, а 4 - в последовательность и связующее дерево.
Шаг 3: Исследуется один из смежных узлов 4 и, таким образом, 4 помещается в стек, а 3 входит в последовательность и связующее дерево.
Шаг 4: Соседние узлы 3 исследуются путем помещения его в стек и 10 входит в последовательность. Поскольку нет смежного узла с 10, таким образом, 3 выталкивается из стека.
Шаг 5: Исследуется еще один соседний узел 3, и 3 помещается в стек, а 9 посещается. Нет смежного узла 9, таким образом, 3 выталкивается, и последний соседний узел 3, то есть 2, посещается.
Аналогичный процесс выполняется для всех узлов, пока стек не станет пустым, что указывает на условие остановки для алгоритма обхода. - -> пунктирные линии в связующем дереве относятся к задним краям, присутствующим на графике.
Таким образом, все узлы в графе проходят без повторения каких-либо узлов.
Преимущества и недостатки
- Преимущества: Это требования к памяти для этого алгоритма очень меньше. Меньшая сложность пространства и времени, чем у BFS.
- Недостатки: решение не гарантируется. Топологическая сортировка. Нахождение мостов графа.
Пример реализации алгоритма DFS
Ниже приведен пример реализации алгоритма DFS:
Код:
import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)
Выход:
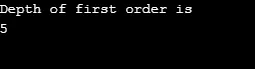
Пояснение к вышеприведенной программе: мы создали график с 5 вершинами (0, 1, 2, 3, 4) и использовали посещенный массив для отслеживания всех посещенных вершин. Затем для каждого узла, соседние узлы которого существуют, один и тот же алгоритм повторяется до тех пор, пока не будут посещены все узлы. Затем алгоритм возвращается к вызову вершины и извлекает ее из стека.
Вывод
Потребность в памяти этого графа меньше по сравнению с BFS, так как требуется только один стек. Связующее дерево DFS и последовательность обхода создаются в результате, но не являются постоянными. Возможна множественная последовательность прохождения в зависимости от начальной вершины и выбранной вершины исследования.
Рекомендуемые статьи
Это руководство по алгоритму DFS. Здесь мы обсудим пошаговое объяснение, пройдемся по графику в табличном формате с преимуществами и недостатками. Вы также можете просмотреть другие наши статьи, чтобы узнать больше -
- Что такое HDFS?
- Алгоритмы глубокого обучения
- Команды HDFS
- Алгоритм SHA