
Введение в биномиальное распределение в R
В этой статье описывается, как использовать биномиальные распределения в R для нескольких операций, связанных с вероятностными распределениями. Бизнес-анализ использует биномиальную вероятность для сложной проблемы. R имеет множество встроенных функций для вычисления биномиальных распределений, используемых в статистической интерференции. Биномиальное распределение, также известное как испытания Бернулли, принимает два типа успеха p и неудачи S. Основная цель модели биномиального распределения состоит в том, чтобы они вычисляли возможные вероятные результаты, отслеживая определенное количество положительных возможностей, повторяя процесс определенное количество раз., У них должно быть два возможных результата (успех / неудача), поэтому результат дихотомичен. Предварительно определенная математическая запись: p = success, q = 1-p.
Есть четыре функции, связанные с биномиальными распределениями. Это дбином, пбином, кбином, рбином. Форматированный синтаксис приведен ниже:
Синтаксис
- дбином (х, размер, проб)
- пбином (х, размер, проба)
- qbinom (x, размер, prob) или qbinom (x, размер, prob, lower_tail, log_p)
- рбином (х, размер, проб)
Функция имеет три аргумента: значение x - это вектор квантилей (от 0 до n), size - количество попыток трейлов, prob обозначает вероятность каждой попытки. Давайте посмотрим один на один с примером.
1) dbinom ()
Это функция плотности или распределения. Значения вектора должны быть целым числом, не должно быть отрицательным числом. Эта функция пытается найти номер успеха в нет. испытаний, которые являются фиксированными.
Биномиальное распределение принимает размер и значения х. например, размер = 6, возможные значения x равны 0, 1, 2, 3, 4, 5, 6, что подразумевает P (X = x).
n <- 6; p<- 0.6; x <- 0:n
dbinom(x, n, p)
Выход:
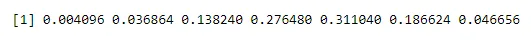
Делая вероятность одному
n <- 6; p<- 0.6; x <- 0:n
sum(dbinom(x, n, p))
Выход:
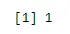
Пример 1 - Больничная база данных показывает, что пациенты, страдающие от рака, умирают от него 65%. Какова вероятность того, что из 5 случайно выбранных пациентов из 3 выздоровеют?
Здесь мы применяем функцию dbinom. Вероятность того, что 3 восстановится с использованием распределения плотности во всех точках.
n = 5, р = 0, 65, х = 3
dbinom(3, size=5, prob=0.65)
Выход:

Для значения х от 0 до 3:
dbinom(0, size=5, prob=0.65) +
+ dbinom(1, size=5, prob=0.65) +
+ dbinom(2, size=5, prob=0.65) +
+ dbinom(3, size=5, prob=0.65)
Выход:
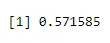
Затем создайте образец из 40 статей и увеличьте на 2, создавая биномиальную форму с использованием dbinom.
a <- seq(0, 40, by = 2)
b <- dbinom(a, 40, 0.4)
plot(a, b)
После выполнения вышеприведенного кода он выдает следующий вывод: биномиальное распределение строится с использованием функции plot ().
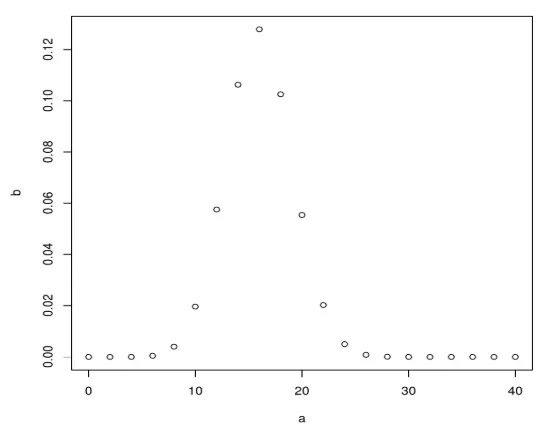
Пример 2. Рассмотрим сценарий. Предположим, что вероятность того, что студент одолжит книгу из библиотеки, составляет 0, 7. В библиотеке 6 студентов, какова вероятность того, что 3 из них одолжат книгу?
здесь P (X = 3)
Код:
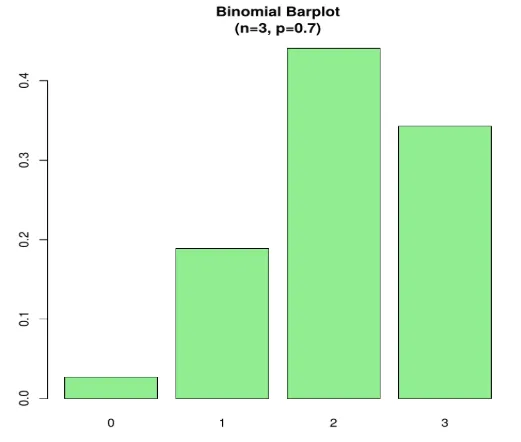
n=3; p=.7; x=0:n; prob=dbinom(x, n, p);
barplot(prob, names.arg = x, main="Binomial Barplot\n(n=3, p=0.7)", col="lightgreen")
На графике ниже показано, когда p> 0, 5, поэтому биномиальное распределение имеет положительный сдвиг, как показано.
Выход:
2) Pbinom ()
рассчитывает совокупные вероятности биномиального или CDF (P (X <= x)).
Пример 1:
x <- c(0, 2, 5, 7, 8, 12, 13)
pbinom(x, size=20, prob=.2)
Выход:

Пример 2: Дравид забивает калитку на 20% своих попыток, когда он играет в шары. Если он будет играть 5 раз, какова вероятность того, что он наберет 4 или меньше калитки?
Здесь вероятность успеха равна 0, 2, и за 5 попыток мы получаем
pbinom(4, size=5, prob=.2)
Выход:
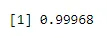
Пример 3: 4% американцев - черные. Найти вероятность 2 чернокожих учеников при случайном выборе 6 учеников из класса 100 без замены.
Когда R: x = 4 R: n = 6 R: p = 0. 0 4
pbinom(4, 6, 0.04)
Выход:-
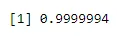
3) qbinom ()
Это квантильная функция, которая выполняет обратную функцию кумулятивной вероятности. Совокупное значение совпадает со значением вероятности.
Пример: Сколько хвостов будет иметь вероятность 0, 2, когда монету подбрасывают 61 раз.
a <- qbinom(0.2, 61, 1/2)
print(a)
Выход:-
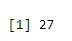
4) rbinom ()
Он генерирует случайные числа. Разные результаты дают разные случайные результаты, используемые в процессе моделирования.
Пример:-
rbinom(30, 5, 0.5)
rbinom(30, 5, 0.5)
Выход:-

Каждый раз, когда мы выполняем, это дает случайные результаты.
rbinom(200, 4, 0.4)
Выход:-

Здесь мы делаем это, предполагая результат 30 бросков монет за одну попытку.
rbinom(30, 1, 0.5)
Выход:-
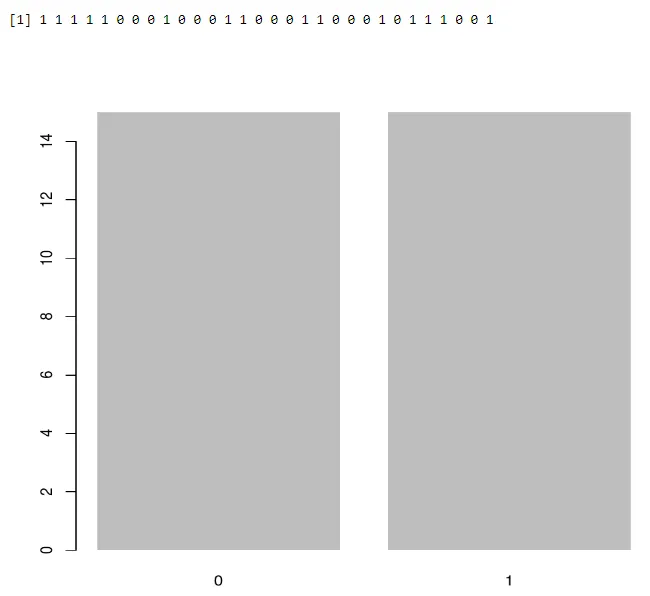
Используя барплот:
a<-rbinom(30, 1, 0.5)
print(a)
barplot(table(a),>
Выход:-
Чтобы найти средство успеха
output <-rbinom(10, size=60, 0.3)
mean(output)
Выход:-
Заключение - биномиальное распределение в R
Следовательно, в этом документе мы обсудили биномиальное распределение в R. Мы смоделировали, используя различные примеры в R studio и R snippets, а также описали встроенные функции, помогающие в генерации биномиальных вычислений. Для вычисления биномиального распределения в R используются статистические расчеты. Следовательно, биномиальное распределение помогает найти вероятности и случайный поиск с использованием биномиальной переменной.
Рекомендуемые статьи
Это руководство по биномиальному распределению в R. Здесь мы обсудили введение и его функции, связанные с биномиальным распределением, а также синтаксис и соответствующие примеры. Вы также можете просмотреть наши другие предлагаемые статьи, чтобы узнать больше -
- Биноминальная формула распределения
- Экономика против Бизнеса
- Методы бизнес-аналитики
- Дистрибутивы Linux