Введение в функцию Sum в Matlab

MATLAB - это язык, используемый для технических вычислений. Как многие из нас согласятся, простая в использовании среда необходима для интеграции задач вычислений, визуализации и, наконец, программирования. MATLAB делает то же самое, предоставляя среду, которая не только проста в использовании, но и решения, которые мы получаем, отображаются в виде математических обозначений, с которыми большинство из нас знакомо. В этой статье мы подробно рассмотрим функцию Sum в Matlab.

Использование Matlab включает (но не ограничивается)

  • вычисление
  • Разработка алгоритмов
  • моделирование
  • моделирование
  • макетирования
  • Аналитика данных (Анализ и Визуализация данных)
  • Инженерная и научная графика
  • Разработка приложения

MATLAB предоставляет своему пользователю корзину функций, в этой статье мы разберемся с мощной функцией под названием «Функция суммы».

Синтаксис:

S = sum(A)

S = sum(A, dim)

S = sum(A, vecdim)

S = sum(__, outtype)

S = sum(__, nanflag)

Описание функции суммы в Matlab

Теперь давайте поймем все эти функции одну за другой.

1. S = сумма (A)

  • Это вернет сумму всех элементов 'A' по измерению массива, который не является одноэлементным, то есть размер не равен 1 (будет учитываться первое измерение, которое не является одноэлементным).
  • sum (A) вернет сумму элементов, если A является вектором.
  • sum (A) вернет вектор строки, который будет иметь часть каждого столбца, если A является матрицей.
  • Если A является многомерным массивом, сумма (A) будет работать вдоль 1-го измерения массива, размер которого не равен 1, и будет рассматривать все элементы как векторы. Это измерение станет 1, а размер других измерений не будет изменен.

Теперь давайте разберем сумму (A) с примером. Но перед этим, пожалуйста, имейте в виду, что в MATLAB матрицы имеют следующие размеры:

1 = строки, 2 = столбцы, 3 = глубина

Пример № 1 - Когда у нас есть строки и столбцы

Как объяснено выше, сумма (A) выполнит сложение по 1-му измерению, которое не является одиночным. Для отдельной строки / столбца мы получим результат в виде одного числа.

A = (1, 3, 7 ; 5, -8, 1);
S = sum(A);

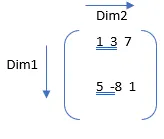
Примечание : здесь S - итоговая сумма, а A - массив, сумма которого нам нужна. A =

Здесь 1 - первое не синглетонное измерение (измерение, длина которого не равна 1). Таким образом, некоторые будут вместе с элементами строки, т.е.

S = сумма (A) = 6 -5 8

Пример № 2 - Когда у нас есть только 1 строка

A = (2, 3, 7 );
B = sum(A);

Здесь первое не одноэлементное измерение равно 2 (т.е. столбцы). Таким образом, сумма будет вместе с элементами столбца

B = сумма (A) = 12

Пример № 3 - Когда у нас есть только 1 столбец

A = (2 ; 5);

Итак, А =

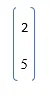
Здесь первое не синглетное измерение равно 1, поэтому сумма будет вместе с элементами строки.

B = сумма (A) = 7

2. S = сумма (A, тусклый)

Эта функция будет возвращать сумму по измерению, переданному в аргументе.

пример

A = (2 4 3; 5 3 6; 7 2 5)

Итак, А =

S = сумма (A, 2)

Здесь мы передали '2' в качестве аргумента, поэтому сумма будет по измерению 2.
Итак, S =

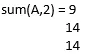
3. S = сумма (A, vecdim)

Эта функция будет суммировать элементы на основе измерений, указанных в векторе 'vecdim'. Например, если у нас есть матрица, то сумма (A, (1 2)) будет суммой всех элементов в A, потому что каждый элемент матрицы A будет содержаться в срезе массива, определенного измерениями 1 и 2 ( Помните, что измерение 1 для строк и 2 для столбцов)

пример

A = ones(3, 3, 2); (Это создаст трехмерный массив, все элементы которого равны 1)

Теперь, чтобы суммировать все элементы, присутствующие в каждом срезе матрицы A, нам нужно указать размеры, которые мы хотим суммировать (и строку, и столбец). Мы можем сделать это, предоставив векторное измерение в качестве аргумента. В нашем примере оба среза представляют собой матрицу 3 * 3, поэтому сумма будет 9.

S1 = сумма (A, (1 2))
Итак, S1 = S1 (:, :, 1) = 9
&
S1 (:, :, 2) = 9

4. S = сумма (A, тип)

Эта функция вернет сумму с типом данных, переданным в аргументе. 'Outtype' может быть 'native', 'default' или 'double'.

пример

A = int32(5: 10);
S = sum(A, 'native')

Выход для этого будет,

S = int32
45

Где int32 - собственный тип данных элементов A, а 45 - сумма элементов от 5 до 10.

5. S = сумма (нанфлаг)

Это будет указывать, нужно ли нам включать или опускать NaN в наших расчетах.

сумма (A, «включая») будет включать все значения NaN, которые присутствуют в расчете.

sum (A, 'omitnan') будет игнорировать все значения NaN.

пример

A = (1 -5 3 -2 NaN 4 NaN 9);
S = sum(A, 'omitnan')

Итак, результат, который мы получим
S = 10
(После игнорирования всех значений NaN)

Вывод

Итак, как мы видим, MATLAB - это система, основным элементом данных которой является массив, который не требует каких-либо измерений. Это позволяет нам решать вычислительные проблемы, особенно проблемы с матричными и векторными формулировками. Все это делается за значительно меньшее количество времени по сравнению с написанием программы на скалярном и неинтерактивном языке, таком как C.

Рекомендуемые статьи

Это руководство по суммированию в Matlab. Здесь мы обсуждаем использование Matlab, синтаксис, примеры вместе с описанием функции суммы в Matlab. Вы также можете посмотреть следующие статьи, чтобы узнать больше

  1. Векторы в Matlab
  2. Функции передачи в Matlab
  3. Matlab Operators
  4. Что такое Matlab?
  5. Matlab Compiler | Приложения Matlab Compiler

Категория:

Большое количество данных