Excel NORMSINV (Содержание)
- Введение в Excel NORMSINV
- Как использовать формулу NORMSINV в Excel?
Введение в Excel NORMSINV
Функция обратного нормального кумулятивного распределения в excel является важным инструментом, который возвращает обратное нормальное кумулятивное распределение для данного значения вероятности, т.е. обычно возвращает обратное значение стандартного нормального кумулятивного распределения (которое имеет среднее значение, равное нулю, и стандартное отклонение, равное единице). Функция NORM.S.INV впервые представлена в Microsoft Excel версии 2010, которая является обновленной версией функции NORMSINV в Excel 2013 и последней версией. Функция NORMSINV в основном используется в анализе кредиторской задолженности и финансов.
Синтаксис Excel NORMSINV

Аргумент:
Вероятность - которая является ничем иным, как вероятностью, соответствует нормальному распределению.
Как использовать формулу NORMSINV в Excel?
В Microsoft Excel встроенная функция NORMSINV подразделяется на статистическую функцию, которая показана на снимке экрана ниже (где она вычисляет обратное значение нормального кумулятивного распределения для данной вероятности).
- Перейти в меню формул.
- Нажмите More Function, как показано на скриншоте ниже.

- Выберите статистическую категорию, под которой мы найдем функцию NORM.DIST, как показано ниже.
Пример № 1 - Использование NORM.DIST и NORMSINV
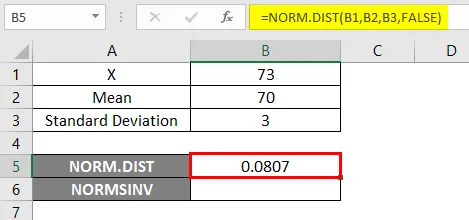
Чтобы использовать функцию NORM.DIST, давайте начнем с простого примера, где нам нужно узнать оценки учеников. Предположим, у нас есть экзамен в классе со средней оценкой 70, то есть mu = 70, и стандартное отклонение класса составляет 3 балла, т.е. сигма = 3 здесь мы должны выяснить, какова вероятность того, что учащиеся получили оценки 73 или ниже, т.е. P (X <= 73). Итак, давайте посмотрим, как узнать вероятность, используя функцию NORM.DIST.
- Х = 3
- Среднее = 70
- Стандартное отклонение = 3
- Примените функцию NORM.DIST, как показано ниже.
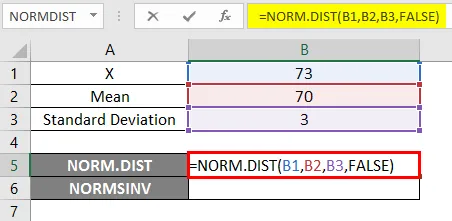
- Если мы применим вышеупомянутую функцию NORM.DIST, мы получим вероятность 0, 0807.
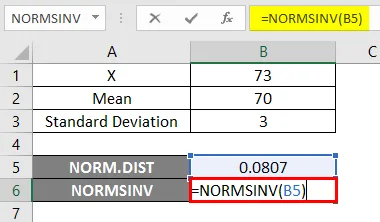
- Теперь примените функцию NORMSINV, чтобы узнать обратное кумулятивное распределение, как показано ниже.
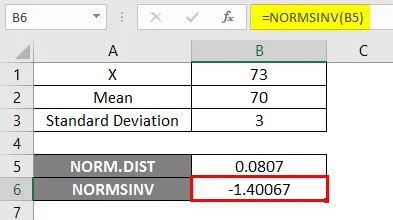
Результат -
В приведенном ниже результате мы видим, что мы получили отрицательные значения -1, 40067 для данной вероятности, т.е.
Пример № 2 - среднее и точное стандартное отклонение
Давайте посмотрим еще один пример с данными на основе кривой, чтобы мы могли узнать среднее и точное стандартное отклонение.
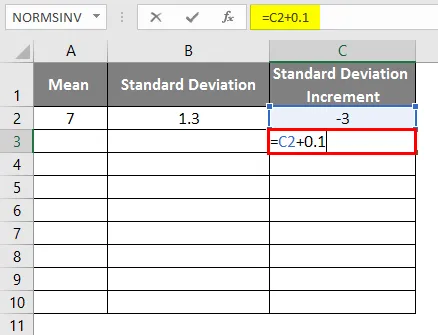
- Среднее = 7
- Стандартное отклонение = 1, 3
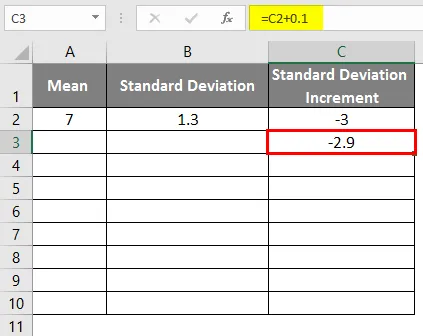
- Увеличение стандартного отклонения как -3

- Чтобы получить кривую колокольчика, мы должны добавить 0, 1 к приращению стандартного отклонения, где данные, как показано ниже.
- После применения формулы результат будет таким, как показано ниже.
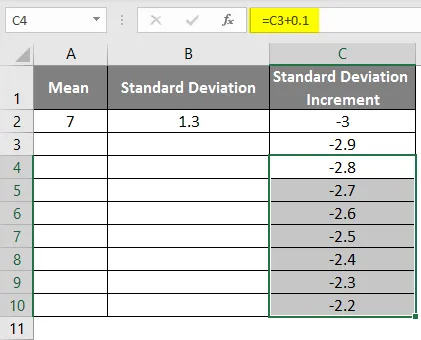
- Перетащите значения, чтобы получить больше значений, пока мы не получим положительные значения, чтобы мы получили левую кривую.
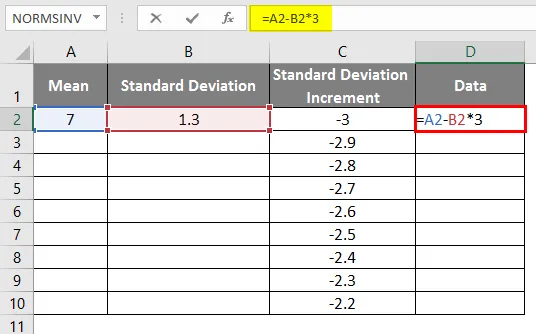
- Чтобы получить правильную кривую, мы должны применить формулу как = среднее стандартное отклонение * 3, чтобы получить точные кривые.
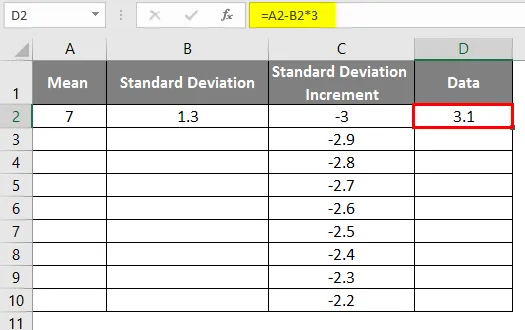
- После использования формулы результат показан ниже.
- Как и в приведенных выше данных для приращения стандартного отклонения, чтобы получить левую кривую, мы увеличили значения на 0, 1
- Тот же сценарий используется путем применения формулы как = 3.1 + STANDARD DEVIATION / 10, чтобы получить приращение кривой 0.1
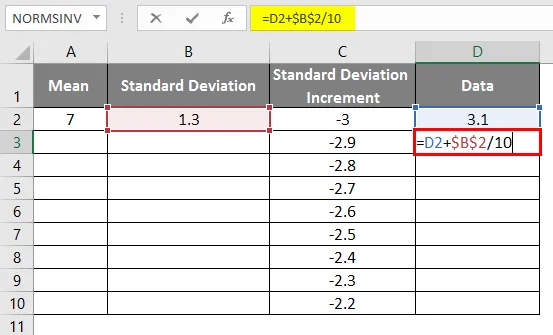
- После использования формулы результат показан ниже.

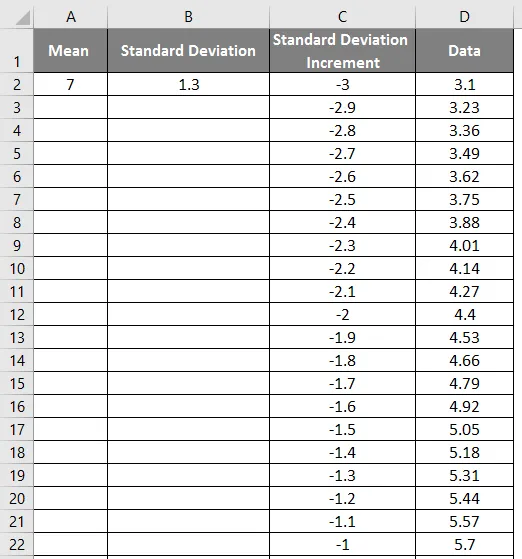
- Перетащите значения, чтобы получить точный результат, который показан на скриншоте ниже.
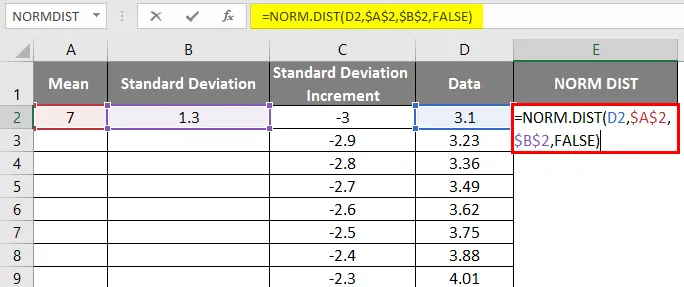
- Теперь примените функцию нормального распределения с формулой = NORM.DIST (значение DATA, среднее значение, стандартное отклонение, false).
- Мы получим следующий результат следующим образом.
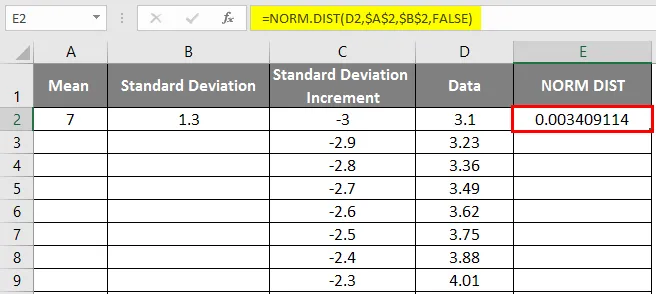
- Перетащите значения, чтобы получить точный результат, который показан ниже.
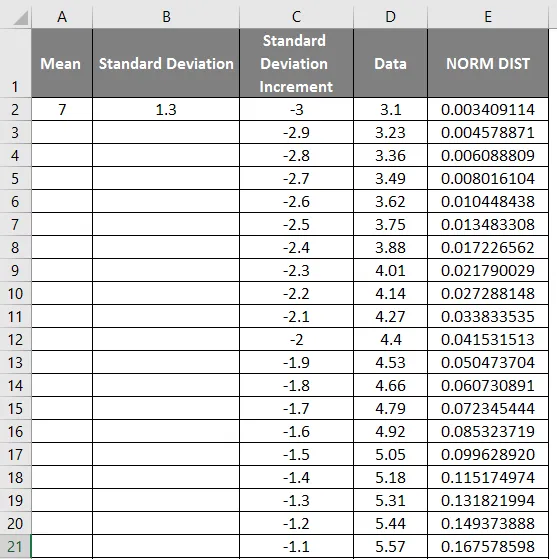
- Как мы можем видеть на скриншоте выше, мы вычислили НОРМАЛЬНОЕ распределение от среднего значения и стандартного отклонения. Теперь давайте посмотрим, что изменится с нормальным распределением, применив NORMSINV, как показано ниже.
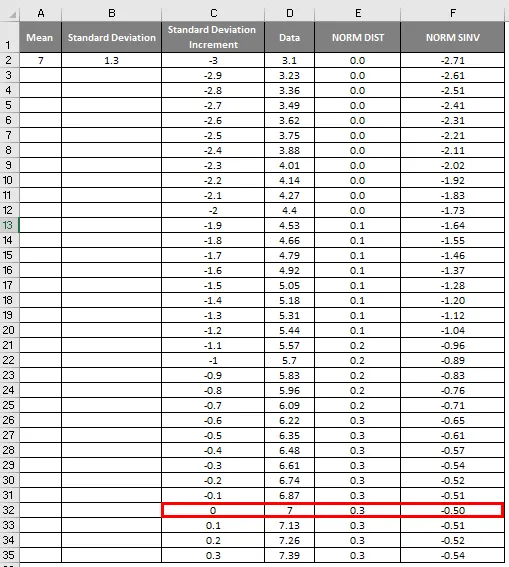
- Здесь мы видим, что значение Zero (0) имеет стандартное отклонение 7.

Применение рассеянного графика, чтобы взглянуть на то, как выглядит левая и правая кривая.
- Сначала выберите данные и столбец Normal.
- Перейдите на вкладку «Вставка» и выберите разбросанный график следующим образом.
- Мы получим график кривой ниже, как показано ниже.
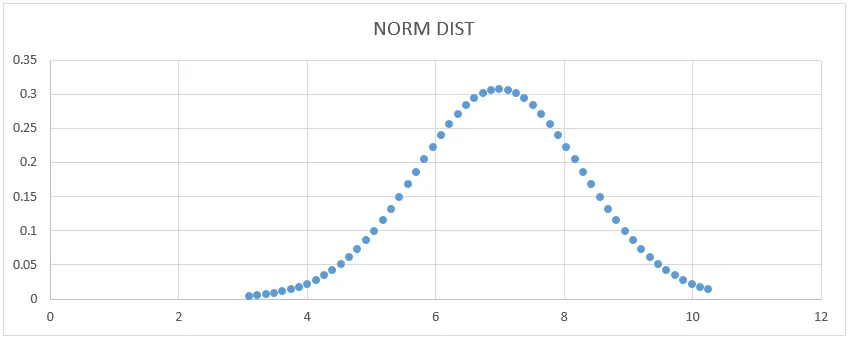
Здесь мы можем видеть, что Среднее значение 7 имеет форму стандартного отклонения, где мы можем показать это, рисуя прямую линию для его представления.
- Среднее = 7
- 1 - стандартное отклонение указывает на 68% данных.
- 2 –стандартное отклонение указывает на 95% данных.
- 3 –стандартное отклонение указывает на 99, 7% данных.
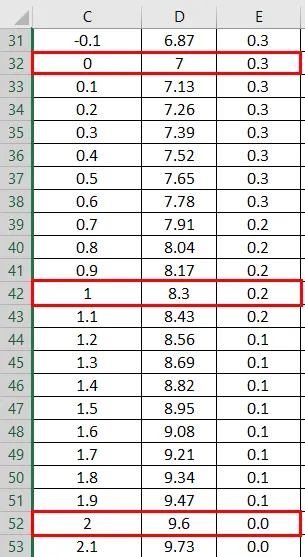
График нормального распределения:
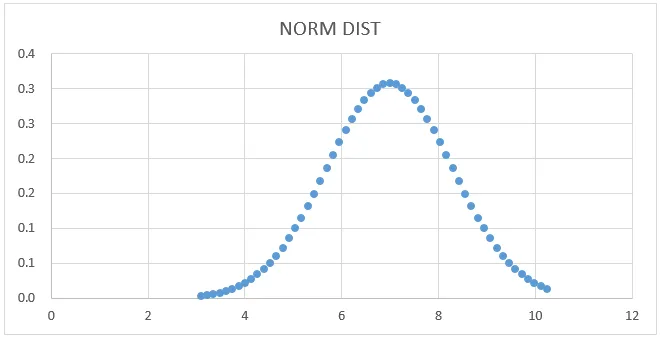
НОРМСИНВ График:
Теперь на приведенном выше рисунке выберите столбец данных и NORM SINV, чтобы получить приведенный ниже график следующим образом.
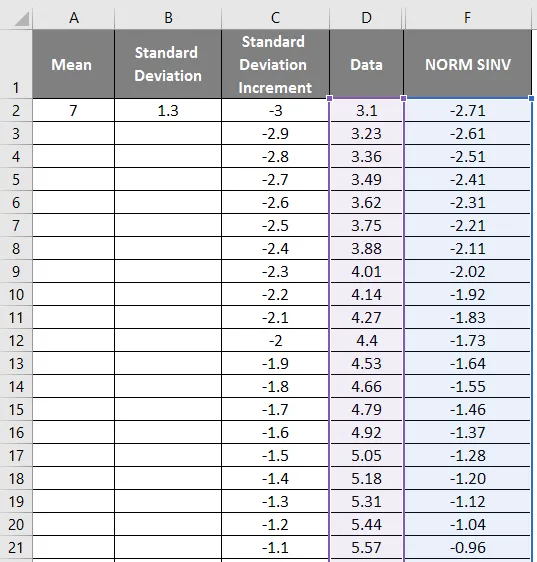
- Сначала выберите данные и столбец Normal.
- Перейдите на вкладку «Вставка» и выберите разбросанный график.
- Мы получим график ниже, который показан на скриншоте ниже.
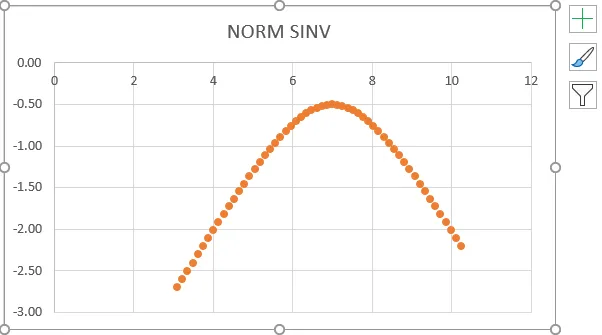
- На приведенном выше снимке экрана мы можем видеть, что мы получили точное обратное значение нормального распределения, которое показывает то же значение, показанное ниже.

Пример № 3 - Настройка левой и правой кривой
В этом примере мы настроим левую и правую кривую, используя нормальную функцию распределения. Рассмотрим приведенные ниже данные, как показано ниже, где x имеет отрицательные значения и увеличивается до положительных значений.
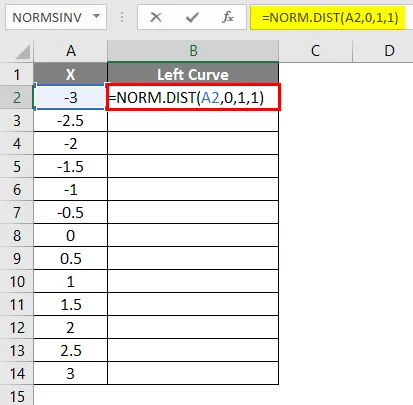
- Применим формулу = NORM.DIST (A2, 0, 1, 1).
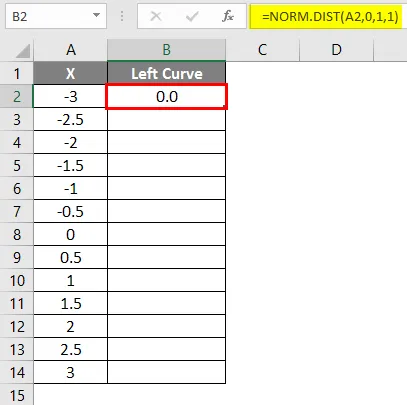
- После применения формулы результат показан ниже.
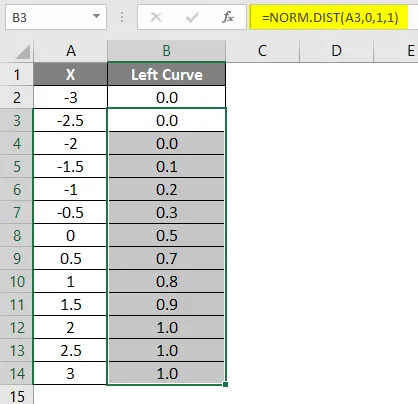
- Перетащите формулу в другие ячейки.
- Применить формулу = 1-B2 .
- После применения формулы результат показан ниже.
- Перетащите ту же формулу в другие ячейки.
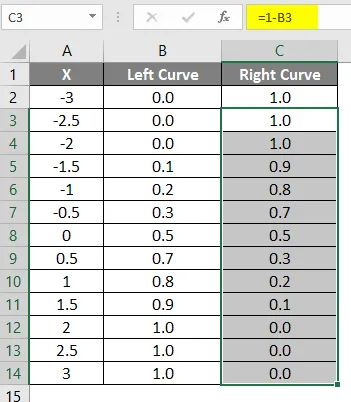
Результат применения вышеуказанной формулы показан ниже.
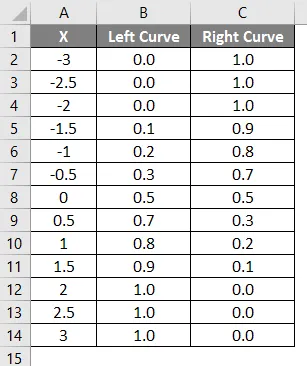
- Значения левой кривой были рассчитаны с использованием формулы НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ, установив совокупное значение как Истина, а NORMSINV был рассчитан с использованием левой кривой.
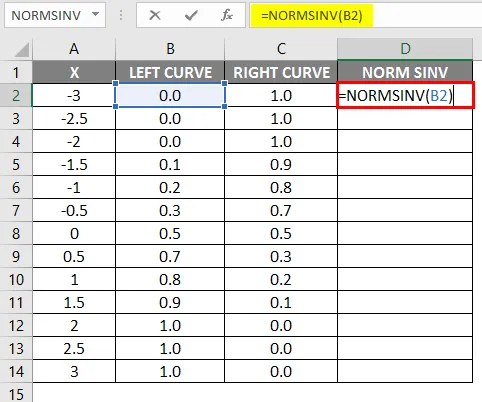
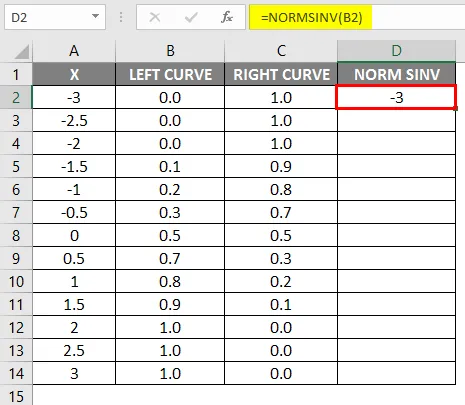
- После применения формулы результат показан ниже.
- Перетащите ту же формулу в другие ячейки.
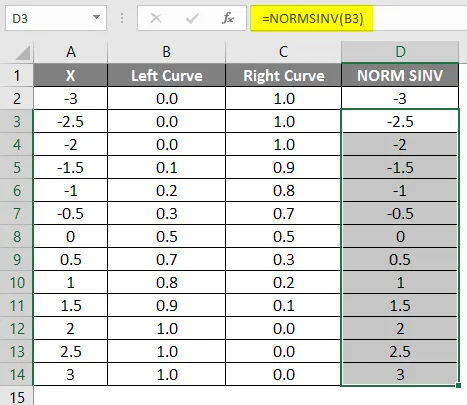
Как мы видим, мы получили то же значение для NORMSINV, которое является ничем иным, как инверсией нормального распределения. Таким же образом, мы получим правильное значение кривой, рассчитав значение 1-левой кривой. На следующем шаге мы собираемся проверить, как мы получим высоту x, используя разбросанный график.
- Выберите левый курс лечения и правый столбец кривой.
- Перейти, чтобы вставить меню.
- Выберите разбросанный график следующим образом.
Мы получим приведенный ниже график, как показано ниже.
НОРМ СИНВ График:
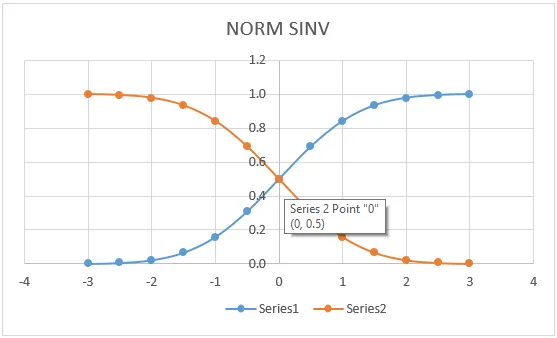
На графике ниже мы видим, что левая кривая значения NORM DISTRIBUTION имеет точное совпадение для (0, 0, 5), которое лежит в центре линии, где мы получим тот же график, если подадим заявку на NORMDIST.
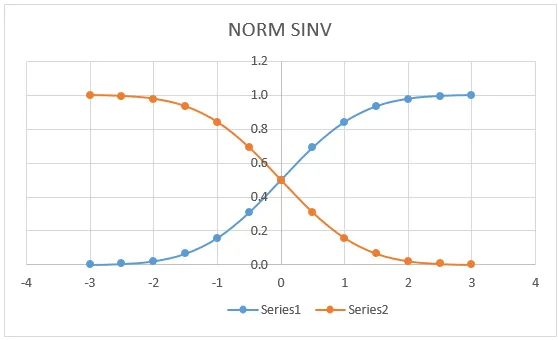
На приведенном выше графике очень четко показано, что мы получили точное среднее значение в центральной точке, которое обозначает:
- Х = 0
- Левая кривая = 0, 5
- Правая кривая = 0, 5
Мы отобразили его, чтобы просмотреть значения NORMSINV в графическом формате, как показано ниже.
Что нужно помнить об Excel NORMSINV
- #значение! Ошибка возникает, когда заданный аргумент не является числовым или логическим значением.
- В функции нормального распределения мы обычно получаем #NUM! ошибка из-за стандартного отклонения аргумента меньше или равна нулю.
Рекомендуемые статьи
Это руководство по Excel NORMSINV. Здесь мы обсудим, как использовать NORMSINV в Excel вместе с практическими примерами и загружаемым шаблоном Excel. Вы также можете просмотреть наши другие предлагаемые статьи -
- Как использовать поле имени в Excel?
- Работа с матрицей в Excel
- Что делать, если анализ в Excel
- NPV Формула в Excel