
Введение в примеры стандартных отклонений
Есть множество примеров стандартных отклонений. Стандартное отклонение - это мера дисперсии набора данных, т. Е. Насколько разбросаны числа. Это полезно для сравнения различных наборов данных, которые могут иметь одинаковое среднее значение, но различный диапазон. Следующий различный пример стандартного отклонения дает представление о наиболее распространенном типе ситуаций, в которых рассчитывается стандартное отклонение, и о том, как его можно вычислить.
Примеры стандартного отклонения
Ниже приведены примеры стандартного отклонения
Стандартное отклонение - пример № 1
Акции компании Z продаются по 50 долларов за акцию, и то же самое предлагает следующие выплаты в следующем году:
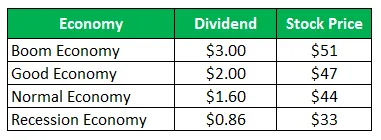
Рассчитайте стандартное отклонение, когда все четыре сценария приведены с равной вероятностью.
Решение:
Расчет возврата периода владения (HPR) выглядит следующим образом -
Формула HPR
HPR = ((Значение на конец периода - Исходное значение) + Доход) / Исходное значение) * 100
Для экономики бум
- HPR (Boom) = ((51-50) + 3) / 50 = 8, 00%
- HPR (хорошо) = ((47-50) + 2) / 50 = -2, 00%
- HPR (нормальный) = ((44-50) + 1, 60) / 50 = -8, 80%
- HPR (рецессия) = ((33-50) + 0, 86) / 50 = -32, 28%
Расчет ожидаемой доходности
Поскольку все сценарии одинаково вероятны, вероятность всех будет ¼
Формула ожидаемого возврата
Ожидаемый доход = (Вероятность бума * Возвращение из бума) + (Вероятность хорошего * Возвращение из хорошего) + (Вероятность нормального * Возвращение из нормального) + (Вероятность рецессии * Возвращение из рецессии)
- Ожидаемый доход = (1/4 x 8%) + (1/4 x -2%) + (1/4 x -8, 80%) + (1/4 x -32, 28%)
- Ожидаемая доходность = -8, 77%
Расчет стандартного отклонения
Формула Разница
Дисперсия = (Вероятность бума * (Возврат с бума - Общая ожидаемая доходность) 2) + (Вероятность хорошего * (Возврат от хорошего - Общая ожидаемая доходность) 2) + (Вероятность нормального * (Возврат от нормального - Общий ожидаемый доход) 2 ) + (Вероятность рецессии * (возврат из рецессии - итоговый ожидаемый доход) 2)
- Дисперсия = 1/4 (8 - (-8, 77)) 2 + 1/4 (-2 - (-8, 77)) 2 + 1/4 (-8.80 - (-8, 77)) 2 + 1/4 (-32, 28 - (-8, 77)) 2
- Дисперсия = 219, 95
Формула стандартного отклонения
Стандартное отклонение будет квадратным корнем дисперсии
Стандартное отклонение = √Variance
- Стандартное отклонение = √ 219, 95
- Стандартное отклонение = 14, 83%
Пример стандартного отклонения - 2
Стандартное отклонение в случае двух компаний в портфеле
Обыкновенные акции Компании А продаются по 28 долларов за акцию, и те же самые предложения предлагаются после выплат в следующем году.

Простые акции Компании B продаются по 93 доллара за акцию, и те же самые предложения предлагают следующие выплаты в следующем году:

(а) Рассчитать стандартное отклонение компании А
(б) Рассчитать стандартное отклонение компании B
(c) Рассчитайте стандартное отклонение портфеля, если половина инвестиций сделана компанией A, а другая половина - компанией B
Решение:
Для компании А
Расчет возврата периода владения (HPR)
Формула HPR
HPR = ((Значение на конец периода - Исходное значение) + Доход) / Исходное значение) * 100
- HPR (бум) = ((20-28) + 1) / 28 = -25, 00%
- HPR (нормальный) = ((30-28) + 1, 50 / 28 = 12, 50%
- HPR (рецессия) = ((38-28) + 5) / 28 = 53, 57%
Расчет ожидаемой доходности компании А
Формула ожидаемого возврата
Ожидаемый доход = (Вероятность бума * Возвращение из бума) + (Вероятность нормального * Возвращение из нормального) + (Вероятность рецессии * Возвращение из рецессии)
- Ожидаемая доходность = (0, 45 х -25, 00%) + (0, 35 х 12, 50%) + (0, 20 х 53, 57%)
- Ожидаемый доход = 3, 84%
Расчет стандартного отклонения компании А
Формула Разница
Дисперсия = (Вероятность бума * (Возврат с бума - Общий ожидаемый доход) 2) + (Вероятность нормального * (Доход от нормального - Общий ожидаемый доход) 2 ) + (Вероятность рецессии * (Возврат из рецессии - Общий ожидаемый доход) 2)
- Дисперсия = 0, 45 (-25, 00 - (3, 84)) 2 + 0, 35 (12, 50 - (3, 84)) 2 + 0, 20 (53, 57 - (3, 84)) 2
- Дисперсия = 895, 15
Формула стандартного отклонения
Стандартное отклонение будет квадратным корнем дисперсии
Стандартное отклонение = √Variance
- Стандартное отклонение = √ 895, 15
- Стандартное отклонение = 29, 92%
Для компании Б
Расчет возврата периода владения (HPR)
Формула HPR
HPR = ((Значение на конец периода - Исходное значение) + Доход) / Исходное значение) * 100
HPR (Boom) = ((200-93) +7) / 93 = 122, 58%
HPR (нормальный) = ((105-93) + 5, 50 / 93 = 18, 82%
HPR (рецессия) = ((4-93) +2) / 93 = -93, 55%
Расчет ожидаемой доходности
Формула ожидаемого возврата
Ожидаемый доход = (Вероятность бума * Возвращение из бума) + (Вероятность нормального * Возвращение из нормального) + (Вероятность рецессии * Возвращение из рецессии)
- Ожидаемая доходность = (0, 45 х 122, 58%) + (0, 35 х 18, 82%) + (0, 20 х -93, 55%)
- Ожидаемый доход = 43, 04%
Расчет стандартного отклонения
Формула Разница
Дисперсия = (Вероятность бума * (Возврат с бума - Общий ожидаемый доход) 2) + (Вероятность нормального * (Доход от нормального - Общий ожидаемый доход) 2 ) + (Вероятность рецессии * (Возврат из рецессии - Общий ожидаемый доход) 2)
- Дисперсия = 0, 45 (122, 58– (43, 04)) 2 + 0, 35 (18, 82– (43, 04)) 2 + 0, 20 (-93, 55– (43, 04)) 2
- Дисперсия = 6783, 65
Формула стандартного отклонения
Стандартное отклонение будет квадратным корнем дисперсии
Стандартное отклонение = √Variance
- Стандартное отклонение = √6783.65
- Стандартное отклонение = 82, 36%
Расчет ожидаемой доходности и стандартного отклонения портфеля, наполовину инвестированного в компанию A, и наполовину в компанию B.
Стандартное отклонение компании А = 29, 92%
Стандартное отклонение компании B = 82, 36%
Вес компании А = 0, 50
Вес компании B = 0, 50
Формула стандартного отклонения портфеля
Стандартное отклонение портфеля = (вес компании A * ожидаемый доход компании A) + ((вес компании B * ожидаемый доход компании B)
- Стандартное отклонение портфеля = (0, 50 * 29, 92) + (0, 50 * 82, 36)
- Стандартное отклонение портфеля = 56, 14%
Анализ
Стандартное отклонение портфеля ниже, чем для отдельных акций, потому что акции диверсифицированы по разным акциям. Диверсификация ведет к снижению риска, если не существует идеальной корреляции между доходностью портфельных инвестиций.
Вывод - примеры стандартных отклонений
Стандартное отклонение измеряет дисперсию набора данных относительно его среднего значения. Он рассчитывается как квадратный корень дисперсии. Чем больше стандартное отклонение ценной бумаги, тем больше будет разница между каждой ценой и средним значением, что показывает, что диапазон цен велик. Вышеупомянутые примеры являются некоторыми из примеров стандартного отклонения по-разному. Существуют и другие примеры, которые показывают, что стандартное отклонение может быть рассчитано с использованием других данных.
Рекомендуемые статьи
Это было руководство к стандартным примерам отклонений. Здесь мы обсуждаем различные примеры стандартного отклонения вместе с подробным объяснением . Вы также можете взглянуть на следующие статьи, чтобы узнать больше -
- Пример с фиксированными затратами
- Пример переменной стоимости
- Пример количественного исследования
- Примеры монополистической конкуренции