
Введение в комплексные числа в MATLAB
Комплексные числа представляют собой комбинацию действительных чисел и мнимых чисел в форме p + qi, где p и q - действительные числа, а i - мнимое число. Мнимое число определяется, где i является результатом уравнения a 2 = -1. Мы можем использовать i или j для обозначения мнимых единиц. Поскольку комплексные числа используются в любых математических вычислениях, а Matlab в основном используется для выполнения математических вычислений. Таким образом, комплексные числа составляют важную часть изучения Matlab.
Генерация комплексных чисел в MATLAB
Сложные числа могут быть созданы или объявлены в Matlab с помощью «сложной» функции. Мы также можем создать комплексные числа, найдя квадратный корень любого отрицательного числа. В Matlab мы можем использовать i или j для обозначения мнимой части комплексного числа.
Примеры
X = 4 + 5i
Здесь X - комплексное число, которое содержит 2 части, то есть действительную и мнимую части. 4 - это действительная часть, а 5 - мнимая часть. Мы можем найти действительные и мнимые части, используя функции в Matlab.
- a = real (X) = 4 (это дает действительную часть комплексного числа)
- b = imag (X) = 5 (это дает мнимую часть комплексного числа)
- complex (6, 7) = 6 + 7i (эта функция используется для создания комплексного числа)
Мы также можем создавать сложные массивы в Matlab, которые также могут быть объявлены с использованием сложных функций.
- а = комплекс (х, у)
Есть определенные условия для x и y, которым мы должны следовать, например, x и y не должны быть одинарными или двойными. Сложный скаляр может быть создан, если два входа имеют скалярный характер, например,
- Х = сложный (5, 3)
- X = 5, 0000 + 3, 0000i
Аналогично, сложный вектор может быть создан, если у нас есть два входа в качестве векторов.
- Х = uint8 ((4; 5; 6; 7));
- Y = uint8 ((3; 5; 1; 2));
- а = комплекс (X, Y)
4 + 3i
5 + 5i
6 + 1i
7 + 2i
Мы можем создать комплексное число, имеющее только один скаляр, как,
- Х = сложный (10)
- X = 10, 0000 + 0, 0000i
Существуют определенные условия, которым должны следовать входные и выходные аргументы:
Входные аргументы содержат действительные и мнимые части, такие как x any y. x и y должны быть скалярными, векторными, многомерными массивами или матрицами в MATLAB. Размер х и у должен быть одинаковым. Они должны иметь один и тот же тип данных, но есть несколько исключений, например, двойное можно использовать с одинарным, а целое число можно объединить со скалярным двойным.
Выходной массив может быть векторным, скалярным, матричным или многомерным массивом в зависимости от входных аргументов. Размер вывода должен совпадать с размером ввода. Если входные аргументы имеют типы данных, отличные от выходных,
- Если какой-либо из входных аргументов имеет одинарный характер, выходные данные также должны быть единичными.
- Если любой из входных аргументов имеет целочисленный характер, то выходные данные должны быть целочисленного типа данных.
Мы можем проверить, является ли матрица действительной или мнимой, используя функцию isreal.
Код:
X = (2+i, 1);
Isreal(X)
Выход:

Код:
Isreal (X (2))
Выход:
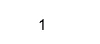
Чтобы извлечь действительные и мнимые части, мы можем использовать реальные и воображаемые функции в Matlab, как,
Код:
real(X)
Выход:
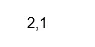
Код:
imag(X)
Выход:

Операции и функции комплексных чисел в MATLAB
Есть несколько операций и функций, которые могут быть выполнены с использованием комплексных чисел в Matlab, как
- abs: эта функция используется для нахождения модуля любого комплексного числа в виде p + qi. abs (2 + 3i) = квадратный корень из (2 2 + 3 2) = (13) 0, 5
- угол: чтобы найти фазовый угол комплексного числа.
Есть определенные советы, которые следует соблюдать для правильного функционирования комплексных чисел в Matlab, как,
- Мы должны избегать использования i и j как части любых имен переменных, так как они используются для обозначения мнимых частей комплексного числа.
- Мы должны избегать использования j или i, если мнимая часть равна 1. Вместо этого мы можем использовать 1j или 1i.
- Мы можем создать сложную функцию в Matlab, когда i и j используются в качестве имен переменных в некоторой части, входные аргументы не имеют одинарный или двойной тип, а мнимая часть равна нулю.
Вывод
Комплексные числа используются в математической или инженерной области. Многие реальные или практические применения могут быть описаны с использованием мнимой части комплексных чисел. Таким образом, понимание использования и применения комплексных чисел на различных платформах важно, особенно если вы имеете дело с какой-либо физической или математической областью.
Рекомендуемые статьи
Это руководство по сложным числам в MATLAB. Здесь мы обсуждаем введение и генерацию комплексного числа в Matlab, включая его примеры с работой и функцией. Вы также можете посмотреть следующие статьи, чтобы узнать больше
- Как написать функции в R?
- Создание 3D Матрицы в MATLAB
- Лучшие 4 функции MATLAB
- Особенности и преимущества версий в MATLAB