
Коэффициент определения формулы (Содержание)
- формула
- Примеры
Что такое коэффициент определения формулы?
В статистике коэффициент детерминации, также называемый R 2, представляет собой инструмент, который определяет и оценивает способность статистической модели объяснять и прогнозировать будущие результаты. Другими словами, если в модели есть зависимая переменная y и независимая переменная x, тогда R 2 помогает определить изменение y по вариации x. Это один из ключевых результатов регрессионного анализа, который используется, когда мы хотим предсказать будущее или протестировать некоторые модели со связанной информацией. Значение R 2 лежит между 0 и 1, и чем выше значение R 2, тем лучше будет прогноз и сила модели. R 2 очень похож на коэффициент корреляции, поскольку коэффициент корреляции измеряет прямую связь двух переменных. R2 в основном представляет собой квадрат коэффициента корреляции.
Формула для определения коэффициента:
Существует несколько формул для расчета коэффициента детерминации:
- Использование коэффициента корреляции:
Correlation Coefficient = Σ ((X – X m ) * (Y – Y m )) / √ (Σ (X – X m ) 2 * Σ (Y – Y m ) 2 )
Где:
- X - Точки данных в наборе данных X
- Y - Точки данных в наборе данных Y
- X m - среднее значение набора данных X
- Y m - среднее значение набора данных Y
Так
Coefficient of Determination(R 2 ) = (Correlation Coefficient) 2
- Использование регрессионных выходов
Коэффициент определения (R 2 ) = Объясненная вариация / Общая вариация
Коэффициент определения (R 2 ) = MSS / TSS
Coefficient of Determination (R 2 ) = (TSS – RSS) / TSS
Где:
- TSS - Общая сумма квадратов = Σ (Yi - Ym) 2
- MSS - Модельная сумма квадратов = Σ (Y - Ym) 2
- RSS - Остаточная сумма квадратов = Σ (Yi - Y ^) 2
Y - прогнозируемое значение модели, Yi - i-е значение, а Ym - среднее значение.
Примеры формулы определения коэффициента (с шаблоном Excel)
Давайте рассмотрим пример, чтобы лучше понять расчет коэффициента определения.
Вы можете скачать этот шаблон формулы определения коэффициента Excel здесь - Шаблон формулы определения коэффициента ExcelКоэффициент определения формулы - пример № 1
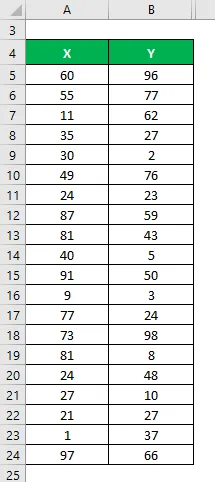
Допустим, у нас есть два набора данных X & Y, каждый из которых содержит 20 случайных точек данных. Рассчитать коэффициент определения для набора данных X & Y.
Среднее значение рассчитывается как:
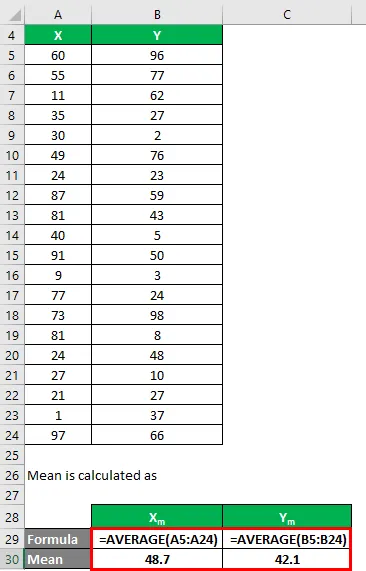
- Среднее из набора данных X = 48, 7
- Среднее из набора данных Y = 42, 1
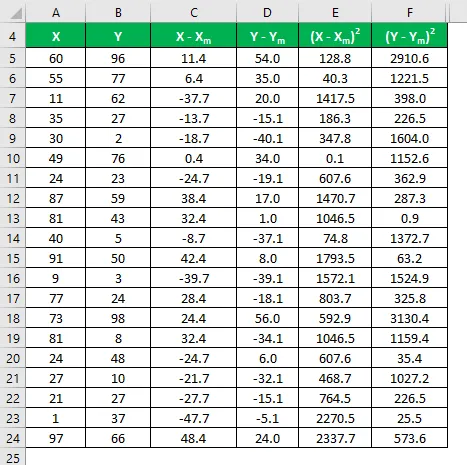
Теперь нам нужно вычислить разницу между точками данных и средним значением.
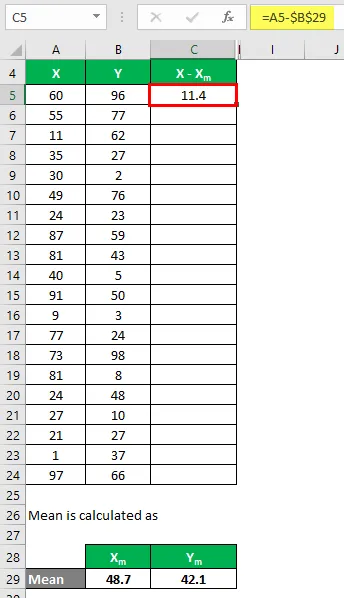
Аналогичным образом рассчитайте для всего набора данных X.
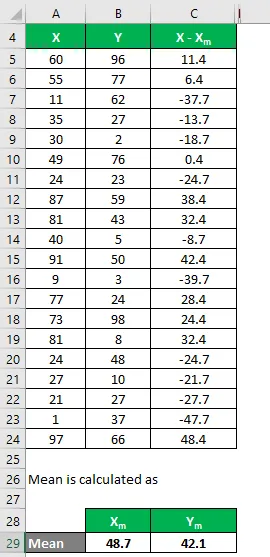
Точно так же вычислите это для набора данных Y также.

Вычислите квадрат разности для обоих наборов данных X и Y.
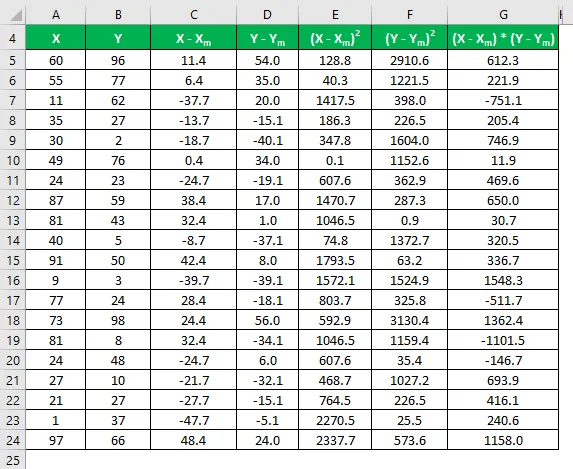
Умножьте разницу в X на Y.
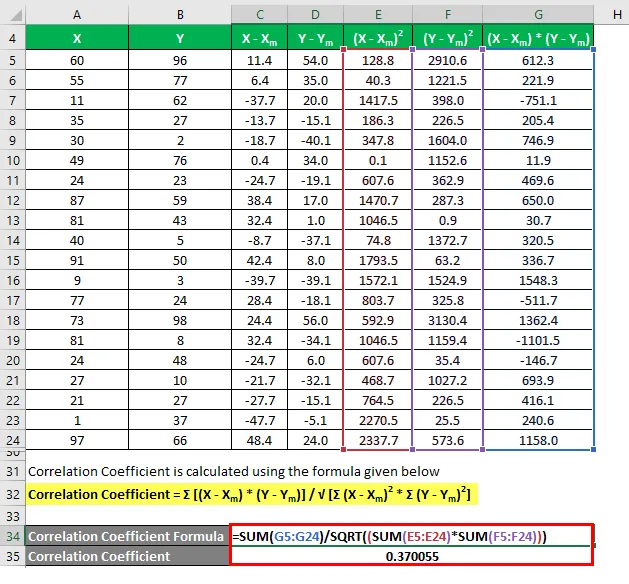
Коэффициент корреляции рассчитывается по формуле, приведенной ниже
Коэффициент корреляции = Σ ((X - X m ) * (Y - Y m )) / √ (Σ (X - X m ) 2 * Σ (Y - Y m ) 2 )
Коэффициент определения рассчитывается по формуле, приведенной ниже
Коэффициент определения = (коэффициент корреляции) 2
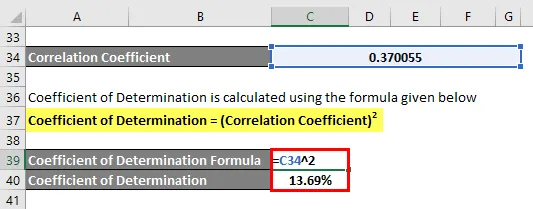
Коэффициент определения = 13, 69%
Коэффициент определения формулы - пример № 2
Допустим, вы очень склонный к риску инвестор и хотите инвестировать деньги в фондовый рынок. Вы не уверены, в какие акции инвестировать, а также у вас низкий аппетит к риску. Таким образом, вы хотите инвестировать в акции, которые безопасны и могут имитировать эффективность индекса. Ваш друг, который является активным инвестором, выбрал для вас 3 акции, основываясь на их фундаментальной и технической информации, и вы хотите выбрать 2 акции из этих трех.
Вы также собрали информацию об их исторических доходах за последние 15 лет.
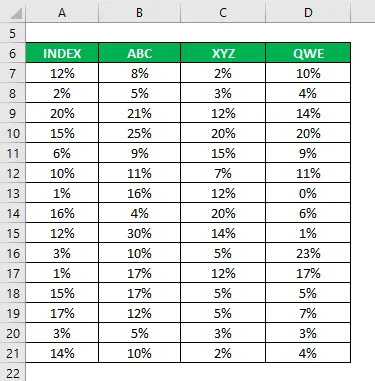
Коэффициент корреляции рассчитывается по формуле Excel
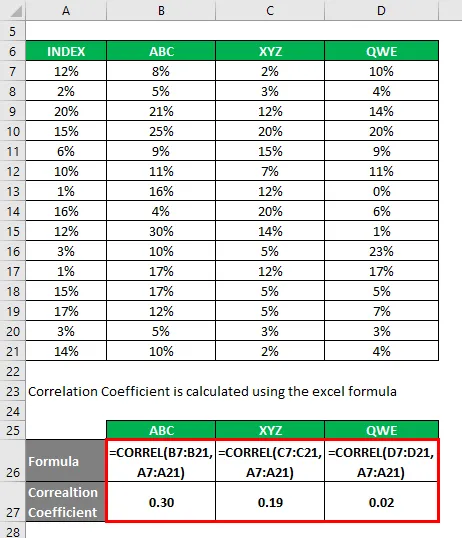
Коэффициент определения рассчитывается по формуле, приведенной ниже
Коэффициент определения = (коэффициент корреляции) 2
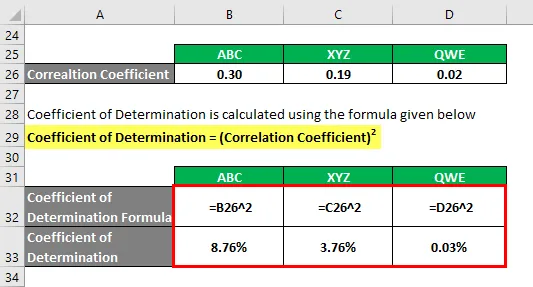
Основываясь на информации, вы выберете акции ABC и XYZ для инвестирования, поскольку они имеют самый высокий коэффициент определения.
объяснение
Коэффициент определения, как объяснено выше, представляет собой квадрат корреляции между двумя наборами данных. Если R 2 равно 0, это означает, что корреляции нет, и независимая переменная не может предсказать значение зависимой переменной. Аналогично, если его значение равно 1, это означает, что независимая переменная всегда будет успешна в прогнозировании зависимой переменной. Но есть и некоторые ограничения. Хотя он говорит нам о корреляции между двумя наборами данных, он не говорит нам, достаточно ли этого значения или нет.
Кроме того, большое значение R 2 не всегда подразумевает, что 2 переменные имеют сильные отношения, и это может быть случайностью. Например: допустим, значение R 2 между количеством автомобилей, проданных за год, и количеством коробок с мороженым, проданных за год, составляет 80%. Но нет никакой связи между этими двумя. Поэтому при использовании R 2 следует быть очень осторожным, сначала понять данные, а затем применить метод.
Актуальность и использование коэффициента формулы определения
Есть много практических применений R 2 . Например, R2 очень часто используется инвесторами для сравнения эффективности своего портфеля с рынком и для того, чтобы попытаться предсказать будущие направления. Аналогично, хедж-фонды, использующие R 2, помогают им моделировать риски в своих моделях. Но в конечном итоге результат основан на чистых цифрах и статистике, которая иногда может вводить в заблуждение. Как упомянуто выше, нужно сначала проверить, имеет ли выход R 2 смысл в реальной жизни или нет.
Рекомендуемые статьи
Это было руководство к коэффициенту формулы определения. Здесь мы обсудим, как рассчитать коэффициент определения, а также на практических примерах и загружаемом шаблоне Excel. Вы также можете посмотреть следующие статьи, чтобы узнать больше -
- Руководство по формуле премии за рыночный риск
- Примеры формулы коэффициента покрытия
- Калькулятор для формулы расчета затрат на основе деятельности
- Как рассчитать соотношение информации по формуле?