
Введение в ряд Фибоначчи в Python
Ряд Фибоначчи в Python, это называется серией чисел, где следующее число является суммой двух существующих чисел.
Например:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 .. также
Так что здесь 0 + 1 = 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
8+ 13 = 21 и так далее.
Глядя на вышесказанное, можно было бы получить определенное представление о том, о чем мы говорим.
Тем не менее, с точки зрения математического правила, оно может быть записано как:

Где n-ое число - сумма числа в местах (n-1) и (n-2). Когда дело доходит до реализации серии Фибоначчи, может быть несколько языков кодирования, с помощью которых это может быть сделано.
Тем не менее, Python является широко используемым языком в наше время. Давайте посмотрим реализацию серии Фибоначчи через Python. Прежде чем продолжить здесь, нужно знать основные условные операторы, такие как цикл, if-else, while и т. Д. В Python. Если нет, было бы замечательно, если бы кто-то мог его пересмотреть, а затем заняться предстоящим содержанием. Здесь для демонстрации я использую spyder, который является IDE для языка программирования Python. Для выполнения программ на Python можно использовать любые другие ноутбуки IDE или Ipython.
Серия Фибоначчи в Python
Давайте посмотрим реализацию числа Фибоначчи и рядов, учитывая, что 1- ые два элемента Фибоначчи - 0 и 1:
Однако вы можете настроить функцию Фибоначчи в соответствии со своими требованиями, но сначала ознакомьтесь с основами и постепенно переходите к другим.
Код Python для поиска n-го числа Фибоначчи
Код 1:
def Fibonacci_num(m):
u = 0
v = 1
if m < 0:
print("Incorrect input entered")
elif m == 0:
return u
elif m == 1:
return v
else:
for i in range(2, m):
c = u + v
u = v
v = c
return v
Код 2:
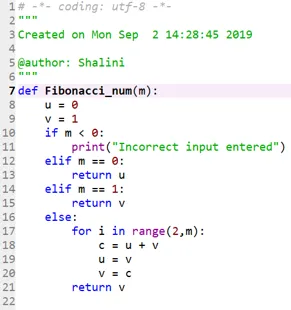
Выход:
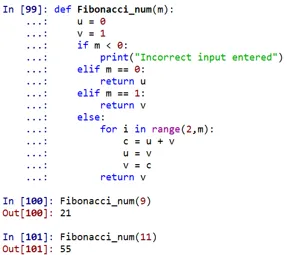
Как можно видеть, число Фибоначчи на 9- м месте будет 21, а на 11- м - 55.
- Здесь «fibonacci_num» - это определенная функция, которая заботится о поиске числа Фибоначчи с помощью определенных условий. Эту функцию можно вызвать, указав любую позицию.
Теперь давайте посмотрим, как можно печатать серии до указанной позиции:
Код:
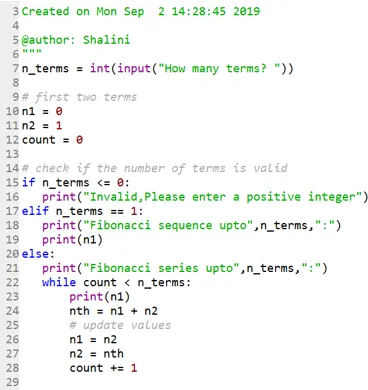
Выход:
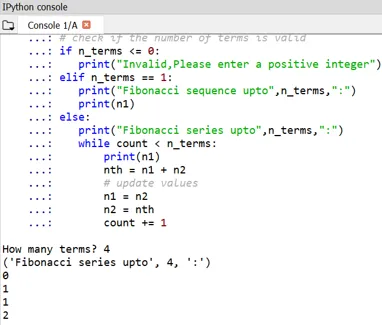
Можно заметить, что начало чисел Фибоначчи определяется как 0 и 1.
- Если кто-то хочет определить свои собственные начальные термины, это также можно сделать аналогичным образом, настроив n1 и n2. Вот пример для этого:
Скажем, теперь мы хотим, чтобы наши начальные условия были: n1 = 3, n2 = 5
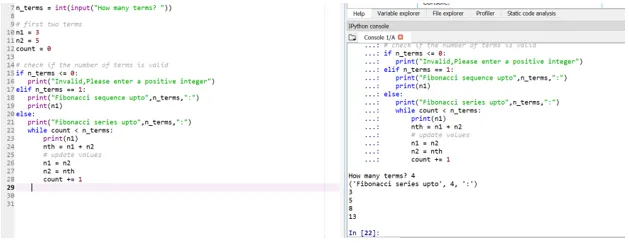
Так что здесь ваша четвертая позиция (пользовательский ввод принимается) будет определяться исходя из ваших начальных условий.
Методы, с помощью которых можно сгенерировать ряд Фибоначчи
Ниже приведены три метода, с помощью которых могут быть сгенерированы ряды Фибоначчи:
1. Через генераторы
Код:
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
Выход:
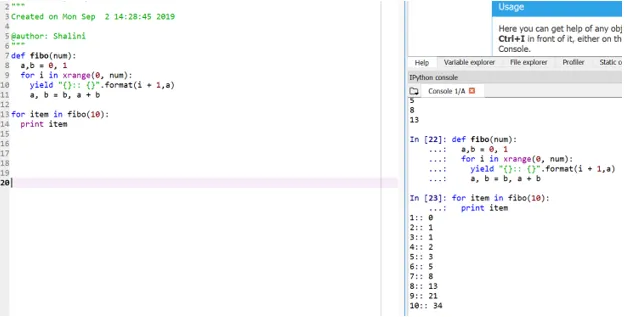
Этот метод называется «генератором», поскольку функция xrange является генератором чисел от 0 до num, а yield является генератором форматированного вывода.
Вот что Xrange делает для вас:

Здесь ряд Фибоначчи был определен в виде функции, внутри которой функции loop, xrange и yield заботятся о выводе.
2. Сквозная петля
Код:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
Выход:

Как можно видеть, простой цикл for использовался для печати ряда Фибоначчи от 0 до 10. Внутри цикла for новым значениям были присвоены переменные. U и v - начальные значения Фибоначчи по умолчанию, которые были установлены в 0 и 1 соответственно.
Что касается выполнения цикла, новое значение u является старым значением v, тогда как новое значение v является суммой старых значений u и v. Это продолжается до конца значений диапазона.
3. Через рекурсию
Код:
#Through recursion
def fibonacci_ser(m):
if(m <= 1):
return m
else:
return(fibonacci_ser(m-1) + fibonacci_ser(m-2))
m = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(m):
print fibonacci_ser(i),
Выход:
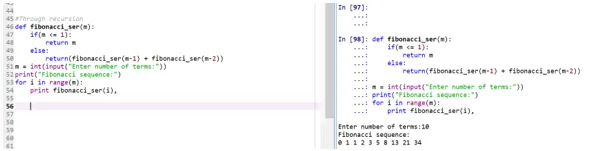
- Функция «fibonacci_ser» вызывает сама себя для вывода ряда Фибоначчи.
- И, следовательно, метод получил название «рекурсия».
Шаги, следующие здесь:
- Здесь пользователю было предложено ввести место, до которого должна быть напечатана серия Фибоначчи.
- Номер проходит через функцию «fibonacci_ser».
- Условие проверяется, если указанная длина меньше 1 или нет. Если да, результат дается сразу.
- Однако, если длина больше 1, рекурсивные вызовы выполняются в «fibonacci_ser» с аргументами, длина которых меньше 1 и 2, то есть fibonacci_ser (m-1) и fibonacci_ser (m-2).
- Следовательно, рекурсия дает желаемый результат и печатает его.
- Итак, вкратце, мы обсудили три способа отображения ряда Фибоначчи.
- Через цикл, через генераторы и через рекурсию.
Все три кода Python суммированы
Ниже приведены три кода Python:
1. Через генераторы
Код:
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
2. Сквозная петля
Код:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
3. Через рекурсию
Код:
def fibonacci_ser(n):
if(n <= 1):
return n
else:
return(fibonacci_ser(n-1) + fibonacci_ser(n-2))
n = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(n):
print fibonacci_ser(i),
Выше перечислены все процедуры, нужно практиковаться, чтобы получить хорошее управление на всех.
Выход:
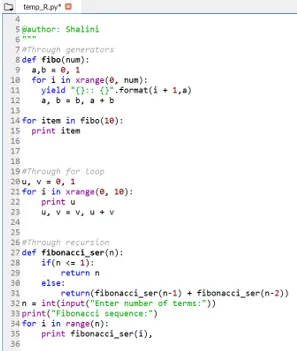
Вывод
Проходя через вышеупомянутое содержание Фибоначчи, можно было бы получить кристально четкое понимание чисел и рядов Фибоначчи, специализирующихся на питоне. Когда-то вы освоитесь с логикой ряда Фибоначчи, генерация другого набора рядов, работа с другими числами и различными методами станет для вас легкой прогулкой. Логический подход - единственный способ преуспеть в этом.
Рекомендуемые статьи
Это руководство к серии Фибоначчи в Python. Здесь мы обсуждаем числа и серии Фибоначчи, специализирующиеся на python, порождающие другой набор рядов, работающие с другими числами и различными методами. Вы также можете просмотреть другие наши статьи, чтобы узнать больше -
- Генератор случайных чисел в Python
- Математические функции в Python
- Факториал в Python
- Инкапсуляция в Python
- Ряд Фибоначчи на Яве
- Особенности Python
- Факториал Программа в JavaScript
- Генератор случайных чисел в Matlab
- Генератор случайных чисел в C #
- Инкапсуляция в JavaScript