
Функция Excel SIN (Содержание)
- Функция SIN в Excel
- Как использовать функцию SIN в Excel?
Функция SIN в Excel
Способность вычислять не охватывает всю математику. Это подраздел, хотя и жизненно важный в его применении. В прошедшие годы это было ограничивающим фактором, за исключением очень известных и чрезвычайно талантливых «человеческих калькуляторов», таких как Шакунтала Деви. Но компьютеры теперь позволяют сделать всю математику более интеллектуальной. Понятия и теоремы математики сейчас важнее, чем когда-либо прежде.
Excel очень искусен в обработке множества математических моделей, вооружен обширным набором математических и логических функций для поддержки различных операций. Он предоставляет целый набор тригонометрических функций, которые помогают нам, когда мы вступаем в мир тригонометрии.
Итак, для решения тригонометрической функции Sine она предоставляет функцию SIN . Это базовая тригонометрическая функция, но она очень полезна, особенно если вы работаете в сфере производства, навигации или связи. Но важно отметить, что Excel использует радианы, а не градусы для вычисления любого тригонометрического выражения. Есть два способа сделать это:
- Напомним, что π = 180 °. Итак, если угол в градусах, умножьте его на π / 180 °, чтобы преобразовать его в радианы. В Excel это преобразование может быть записано как PI () / 180. Например, чтобы преобразовать 60 ° в радианы, выражение для Excel будет равно 60 * PI () / 180, что равно 1, 0472 радиан.
- Excel также оснащен очень полезным инструментом, обычно называемым RADIANS. Он принимает угол в качестве аргумента, в котором угол относится к градусам, которые должны быть преобразованы в радианы. Возьмем случай, когда выражение, которое используется для преобразования 210 ° в радианы, равно «RADIANS (210)», и оно оценивается в 66519 радиан.
Наоборот, утилита DEGREES одинаково важна. Эта функция может использоваться для полной противоположности функции RADIANS путем преобразования радиан в градусы. Как пример, DEGREES (PI () / 2) оценивает 90.
Как использовать функцию SIN в Excel?
Давайте разберемся, как использовать функцию SIN в Excel, используя несколько примеров и реальных иллюстраций функции SIN в Excel.
Вы можете скачать этот шаблон SIN Function Excel здесь - Шаблон SIN Function ExcelФункция SIN в Excel - Пример № 1
Расчет значения синуса с использованием функции SIN в Excel
Чтобы найти синус определенного числа, мы должны сначала написать = SIN () в конкретной ячейке.

Как видно из приведенного выше снимка экрана, функция SIN в Excel ожидает ввод числа. Это число обычно представляет значение в радианах.
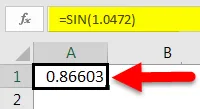
Так что в этом случае мы напишем «= SIN (1.0472)», где 1.0472 - это радианы, эквивалентные 60 градусам.
Как только мы сделаем это, мы получим значение SIN 60 градусов.
Функция SIN в Excel - Пример № 2
Расчет значения синуса с использованием функции SIN и RADIAN в Excel
Теперь давайте посмотрим, как мы можем использовать SIN более продуктивно, в случае, когда мы не знаем точное значение радиана для градуса.
Мы будем использовать RADIANS (), чтобы узнать значение радиана, которое мы передадим в качестве аргумента функции SIN.
Итак, начнем с более ранней версии SIN ():

Далее мы передадим RADIANS (60) в качестве аргумента функции SIN, где 60 - это значение в градусах.

Как видно из приведенного выше примера, RADIANS () принимает значение в градусах. Итак, мы передадим 60 как значение для RADIANS ().

Затем нажмите Enter. Это дает следующий результат.

Итак, мы видим, что результат такой же, как в первом примере.
Функция SIN в Excel - Пример № 3
Расчет значения синуса с использованием SIN и функции PI в Excel
Существует еще один способ преобразования значения градуса в радианы для использования в функции SIN. Из школьного времени мы помним, что π = 180 °. Итак, если угол в градусах, умножьте его на π / 180 °, чтобы преобразовать его в радианы. В Excel это преобразование может быть записано как PI () / 180. Например, чтобы преобразовать 60 ° в радианы, выражение для Excel будет равно 60 * PI () / 180, что равно 1, 0472 радиан.
Давайте посмотрим, как это работает:
Мы начнем с написания функции SIN так же, как описано выше.

Далее мы напрямую передадим 60 ° в качестве аргумента функции SIN. Но это не даст нам соответствующее значение 60 градусов в радианах. Следовательно, мы умножим 60 на PI () / 180.

Это даст нам следующий результат:
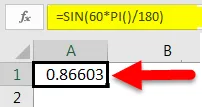
Как мы видим, это то же самое, что и приведенные выше примеры.
Функция SIN в Excel - Пример № 4
Теперь давайте посмотрим на другой пример, показывающий результаты функции SIN для различных значений.

Пояснения к результатам приведены в приведенной выше таблице:
Случай 1 и 2:
3.14 - это значение Pi, и мы можем использовать оба метода, чтобы получить значение 0. Это в основном означает, что SIN для радиан Пи равно 0 .
Случай 3 и 4:
Радианы и Pi / 180 имеют одинаковое значение в математике, и, следовательно, функция SIN дает одинаковое значение. В обоих примерах SIN равен 30 градусам, что дает значение 0, 5.
Случай 5 и 6:
SIN 45 = 0, 85 - это SIN 45 радиан, что означает, что по умолчанию Excel принимает все углы в радианах, а не градусы. Чтобы преобразовать его в градусы, мы можем использовать функцию радиана и получить SIN 45 градусов, как показано в последнем ряду. т.е. SIN (RADIANS (45)) = 0, 707 или 0, 71
Функция SIN в Excel - Пример № 5
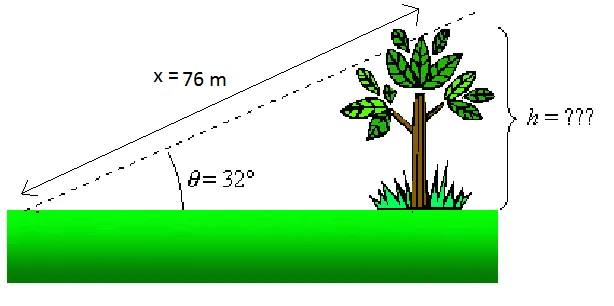
Скажем, например, мы хотим знать высоту дерева на рисунке выше. Мы знаем, что если мы стоим в 76 м от вершины дерева (x = 76 м), то линия визирования к вершине дерева составляет 32 ° по отношению к горизонту (θ = 32 °). Мы знаем это:
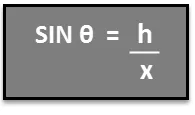
Следовательно, чтобы определить высоту дерева h, находим h = x SIN θ.

Функция SIN имеет только один аргумент, который является числом. Число требуется для расчета SIN этого. Следовательно, очень важно преобразовать градусы в радианы, прежде чем найти синус этого числа.
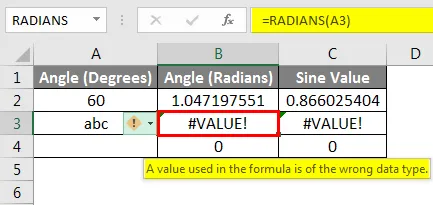
Функция SIN отображает # ЗНАЧЕНИЕ! ошибка, если ссылка, используемая в качестве аргумента функции, указывает на ячейку, содержащую текстовые данные. В приведенном ниже примере ссылка на ячейку третьей строки указывает на текстовую метку в углу (градусы) . Поскольку функции SIN поддерживают только число в качестве аргумента, SIN будет приводить к ошибке, в данном случае, #VALUE!, Если ячейка указывает на пустую ячейку, функция возвращает нулевое значение, как показано в примере ниже. Тригонометрические функции Excel интерпретируют пустые ячейки как ноль, а синус нулевых радиан равен нулю.
Функция SIN в Excel - Пример № 6
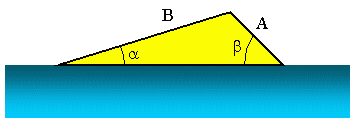
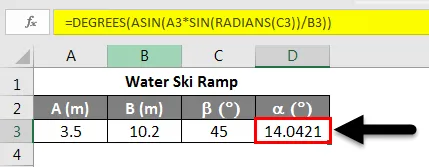
Теперь предположим, что мы хотим узнать угол запуска рампы для водных лыж, как показано на рисунке выше. Мы знаем, что A = 3, 5 м, B = 10, 2 м и b = 45, 0 °. Теперь, чтобы найти, мы можем использовать закон синусов. В этом сценарии это может быть записано как:
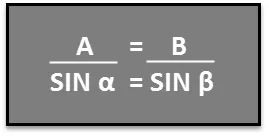
Мы можем реорганизовать это уравнение как:
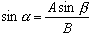
Используя арксинус или обратный синус, мы можем узнать угол α . Применяя уравнение, показанное ниже.

Пример № 7
В нашем последнем тригонометрическом примере мы будем использовать Excel для проверки тригонометрической идентичности:
sin²θ + cos²θ = 1
Обратите внимание, что на скриншоте ниже эта идентичность сохраняется, когда θ задано в радианах и градусах.

Обратите внимание, что описание единицы измерения угла θ находится в разных ячейках, чем числа. Если мы поместим числа и единицы измерения в одну и ту же ячейку, Excel не сможет отличить число от текста, и поэтому мы не сможем ссылаться на ячейки для использования в уравнении, и это приведет к # ЗНАЧЕНИЮ! ошибка.
То, что нужно запомнить
- Имейте в виду, что функция SIN в Excel по умолчанию работает с Radian.
- Преобразуйте число в радианах или градусах, используя функцию RADIANS или DEGREES.
- Вы можете использовать функцию PI (), чтобы получить точные результаты функции SIN при работе с π.
Рекомендуемые статьи
Это было руководство по функции SIN в Excel. Здесь мы обсудили, как использовать функцию SIN в Excel вместе с практическими примерами и загружаемым шаблоном Excel. Вы также можете просмотреть наши другие предлагаемые статьи -
- Важные функции по математике в Excel (Easy)
- Руководство по разделению формулы в Excel
- Важные расширенные формулы и функции Excel
- Шпаргалка по формулам Excel